Теоретические основы гидравлической классификации

Теоретическими основами гидравлической классификации являются закономерности падения минеральных зерен в воде.

Скорость падения частиц в среде зависит от их размеров, формы, плотности зерна и плотности среды. Более крупные частицы с большой плотностью падают быстрее, чем мелкие с малой плотностью. Однако скорость падения крупной частицы с большой плотностью может значительно уменьшиться, если она имеет плоскую форму, так как в этом случае возрастает сопротивление среды.

Различают два основных вида сопротивления среды: динамическое и вязкостное.

На скорость падения частиц при гидравлической классификации влияют оба вида сопротивления, но степень их проявления при падении различных зерен неодинакова.

При падении крупных частиц с большой скоростью преобладает динамическое сопротивление, а при падении мелких частиц – вязкостное.

Конечную скорость падения в воде υ₀ (м/с) зерен крупнее 1 мм можно определить по формуле Риттингера

υ₀ = R 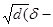1000), (4.1)

где R - числовой коэффициент (для воды R = 0,16, для воздуха R = 4,6); d - диаметр шарообразного зерна, м; δ - плотность зерна, кг/м³.

Для зерен крупностью менее 0,1 мм конечная скорость падения определяется по формуле Стокса

υ₀ = Sd² (δ - 1000), (4.2)

где S - числовой коэффициент (для воды S = 545, для воздуха S = 30278).

Для определения конечной скорости падения зерен промежуточной крупности (0,1 - 1 мм) применима формула Аллена

υ₀ = Ad 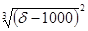, (4.3)

где А - числовой коэффициент (для воды A = 1,146, для воздуха A = 40,6).

Рассчитанные по формулам 4.1 – 4.3 конечные скорости падения зерен шарообразной формы в воде превышают действительные, так как все минеральные зерна, поступающие на гидравлическую классификацию после измельчения, имеют иную форму - плоскую, угловатую, продолговатую, округлую и др.

Универсальный метод определения конечной скорости падения шарообразной частицы в жидкой среде по параметру Рейнольдса, предложен П. В. Лященко. Этот метод

учитывает оба вида сопротивления для любой жидкой среды.

Числом Рейнольдса (Re) называют отношение произве­дения скорости частицы на ее диаметр и плотность жидкости к коэффициенту вязкости жидкости.

Re = 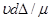, (4.4)

где Re - параметр Рейнольдса (безразмерный); u - относительная скорость движения тела, м/с; d - диаметр движущегося тела, м; А - плотность жидкости, кг/м³; m -коэффициент абсолютной вязкости жидкости, Н·с/м².

При Re > 1000 режим движения жидкости турбулентный, при Re < l - ламинарный и при Re = 1 ÷ 1000 - неустойчивый.

Определение конечной скорости заключается в том, что для из­вестных параметров частицы и среды рассчитывается параметр Re²y по формуле

Re²y = 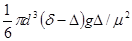, (4.5)

где d - диаметр частицы, м; d - плотность частицы, кг/м³; D - плотность среды (для воды D = 1000 кг/м³); g - ускорение свободного падения (g = 9,81 м/с²); m - коэффициент вязкости воды m = 0,001 Н·с/м²).

Параметр Re²y, впервые предложенный П. В. Лященко,также безразмерный подобно числам Re и y и между ними установлена связь (см. диаграмму рис. 4.1).

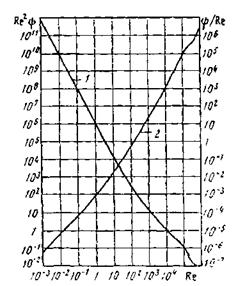
Рис. 4.1. Зависимость параметров Re²y (1) и ψ/Re (2) от Re

На диаграмме (см. рис. 4.1) по рассчитанному значению Re²y находят значение Re, после чего по формуле (4.4)определяют конечную скорость.

Отношение диаметров частиц двух разных минералов, падаю­щих с одинаковой скоростью, на­зывается коэффициентом равнопадаемости.

Коэффициент равнопадаемости показывает, во сколько раз частица легкого минерала больше зерна тяжелого минерала, имеющего одну и ту же конечную скорость падения и определяется для частиц любой крупности по формуле:

е = d₁/d₂ = Re₁/Re₂ » [(d₂ - D)/(d₁ - D)] ⁿ, (4.6)

где d₁ и d₂ - размеры равнопадающих частиц легкого и тяжелого минералов, м; d₁ и d₂ - плотность этих частиц, кг/м³; D - плотность среды, кг/м³; n = 1 ÷ 3.

В практических условиях обогащения частицы движутся не свободно, а в массе и в ограниченном пространстве, т. е. в стесненных условиях.

Скорость стесненного падения частиц всегда меньше скорости свободного падения и зависит от вязкости среды, которая увеличивается с увеличением содержания в ней твердых частиц.

Она может быть выражена формулой

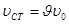(4.7)

где u_ст - конечная скорость падения частиц в жидкости в стесненных условиях, м/с; u₀ - конечная скорость свободного падения частиц, м/с; θ - коэффициент снижения скорости.

Согласно вычислениям, θ = 0,08 ÷ 0,21.

Законы свободного и стесненного падения частиц использо­ваны при разработке процессов гравитационного обогащения, гидроклассификации и осветления шламовых вод.

Дата добавления: 2014-11-01; просмотров: 651; Нарушение авторских прав

Мы поможем в написании ваших работ!