ИССЛЕДОВАНИЕ ПАРАМЕТРОВ ОТКРЫТЫХ ОПТИЧЕСКИХ РЕЗОНАТОРОВ

1. Цель работы

- Ознакомление с геометро-оптическим и волновым описанием поведения оптических колебаний в открытых резонаторах.

- Изучение математического моделирования поля в вакуумированных оптических резонаторах.

- Изучение влияния сред, заполняющих открытый резонатор, на спектр его собственных колебаний.

- Компьютерный анализ амплитудно-фазовых распределений оптических полей собственных колебаний устойчивых и неустойчивых открытых резонаторов.

- Компьютерный анализ спектров собственных колебаний устойчивых открытых резонаторов.

2. Домашнее задание

Повторить разделы высшей математики, касающиеся теории специальных функций. Использовать конспекты лекций по математическому анализу, по электродинамике и распространению радиоволн, по системам атмосферной оптической связи, а также литературу [1-2].

3. Основные теоретические сведения

Назначение оптического резонатора в лазере

Лазер является устройством, автоматически генерирующим (за счет энергии внешнего источника) когерентное электромагнитное излучение оптического диапазона. Поэтому структурная схема лазера должна содержать колебательный контур (резонатор), определяющий частоту выходящего из лазера оптического пучка, его направление, поперечную структуру, форму главного и боковых лепестков диаграммы направленности. К оптическому резонатору, как и обычно к резонансному контуру, предъявляется требование частотной избирательности за счет высокой добротности на одной или нескольких оптических частотах и низкой добротности на других, даже близко расположенных, частотах.

Можно ли создать такой высокодобротный резонатор для света?

Принцип построения СВЧ резонатора «не срабатывает» в оптическом диапазоне. Вспомним, как подобная техническая задача решена в поддиапазоне миллиметровых волн, примыкающем к оптическому со стороны более низких частот. Там эффективные колебательные устройства удалось реализовать в виде полого металлического объема (объемного резонатора). Опираясь на принцип электродинамического подобия, на первый взгляд кажется, что можно напрямую воспользоваться этим опытом, перенеся его в оптический диапазон? Оказалось, что нет, и вот по какой причине. Геометрические размеры полого металлического резонатора (например, имеющего форму параллелепипеда с размерами ребер aЧbЧc) во избежание поддержания СВЧ колебаний одновременно на нескольких частотах, должны быть соизмеримы с длиной волны основного колебания: 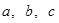~ 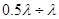. В оптическом диапазоне, где 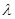измеряется несколькими микрометрами или даже десятыми долями их, такой резонатор невыполним по двум причинам. Первая – чисто технологическая. Вторая – физическая, то есть имеет принципиальный характер. Дело в том, что добротность полого металлического резонатора может быть оценена, как отношение объема, в котором запасается энергия СВЧ колебаний, к объему, в котором она теряется в виде тепла:

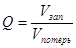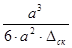~ (1)

При нормальном скин-эффекте толщина скин-слоя, на глубину которого СВЧ поле проникает в металлические стенки резонатора, 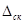~ 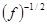, тогда как 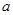~ 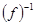. Поэтому ~ 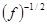, и, поскольку оптические частоты превышают СВЧ

Рис. 1. Иллюстрация сгущения спектра в замкнутом оптическом резонаторе

на четыре порядка и более, добротность одночастотного оптического резонатора упадет по крайней мере в 100 раз.

Тогда, вернув резонатору реальные размеры ( 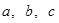- порядка от одного до нескольких сантиметров), мы вынуждены будем согласиться с его многомодовостью, то есть одновременным существованием большого (даже очень большого) числа типов колебаний. Если 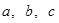во много раз превышают 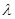, то в каждой единице объема резонатора в единичной полосе частот будет поддерживаться столько же типов колебаний, сколько в свободном пространстве: . Общее число колебаний в резонаторе объемом 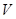в полосе 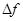составит

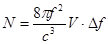. (2)

Тогда, частотный разнос двух соседних типов колебаний составит

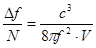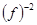~ , (3)

то есть в резонаторе тех же размеров, что и для СВЧ диапазона частотный спектр собственных типов оптических колебаний сгущается по крайней мере в 10⁸ раз! (рис. 1.)

Рис. 2. Амплитудно-частотная характеристика замкнутого оптического резонатора.

Одновременно со сгущением спектра добротность резонатора на каждом более высоком типе колебаний падает, то есть расширяется полоса существования в резонаторе этого типа колебаний:

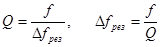, (4)

Согласно (1) ~ , но в большом резонаторе размер 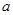уже не зависит от частоты. Поэтому при нормальном скин-эффекте

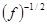~ , (5)

и

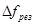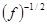~ , (6)

Амплитудно-частотная характеристика резонатора приобретает на оптических частотах следующий вид (рис. 2).

Таким образом, закрытый металлический резонатор не может быть использован в качестве колебательного устройства в оптическом диапазоне частот.

Рис. 3. Геометрия открытого резонатора с прямоугольными зеркалами.

При малых размерах резонатора (сопоставимых с оптической длиной волны) он очень низкодобротен, запасенная в нем энергия слишком мала для практических применений, технологическая реализация его невозможна; при больших размерах резонатора (намного превышающих длину волны оптических колебаний) спектр собственных типов колебаний становится настолько густым, что с учетом снижения добротности колебаний, относящихся к оптическому диапазону, их резонансные полосы перекрываются, сливаясь в сплошной континуум частот: избирательность по частоте закрытого резонатора пропадает, резонатор перестает быть резонатором.

Так возникла проблема: как в полости больших размеров разредить спектр собственных колебаний, чтобы восстановить избирательность на частотах оптического диапазона и вернуть полости резонансные свойства?

Для этого (по предложению академика А. М. Прохорова) пришлось раскрыть полость: удалить четыре боковые стенки, оставив две (размерами a´b) параллельные одна другой и разнесенные на расстояние c (рис. 3).

4. Основные параметры оптических резонаторов

4.1. Добротность закрытого резонатора

Из выражения (1) для вакуумированного резонатора

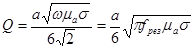, (7)

где

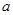- размер ребра внутреннего объема кубического резонатора, м;

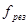- резонансная частота поля в резонаторе, Гц;

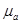- абсолютная магнитная проницаемость материала стенок, Гн/м;

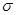- проводимость материала стенок, См/м.

4.2. Ширина резонансной кривой собственных типов колебаний закрытого резонатора

Ширина резонансной кривой может быть получена из выражения (4) (рис. 4)

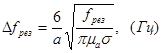. (8)

Рис. 4. Пояснение к рассуждению о ширине резонансной кривой собственных колебаний закрытого резонатора

4.3. Число колебаний в единичной полосе в закрытом резонаторе единичного объема (при 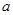>> 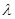) около частоты 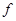(рис. 5):

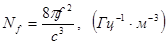. (9)

Рис. 5. Иллюстрация соотношения числа колебаний в закрытом резонаторе единичного объема в СВЧ и оптическом диапазонах.

4.4. Спектральная плотность типов колебаний в закрытом резонаторе больших ( 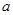>> 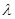) размеров.

Согласно (3),

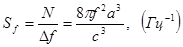, (10)

где

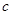- скорость света, м/с;

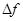- полоса частот (выбирается произвольно), вмещающая 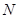типов колебаний закрытого резонатора, Гц.

4.5. Частотный интервал между соседними типами колебаний закрытого резонатора (рис. 6)

,

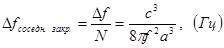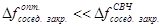. (11)

Рис. 6. Иллюстрация соотношения частотных интервалов между соседними типами колебаний в закрытом резонаторе в СВЧ и оптическом диапазонах.

4.6. Межмодовое расстояние (частотный интервал) двух соседних продольных типов колебаний открытого резонатора (рис. 7)

Рис. 7. Иллюстрация соотношения частотных интервалов между соседними типами колебаний в закрытом резонаторе в СВЧ диапазоне и между двумя соседними продольными типами колебаний открытого резонатора

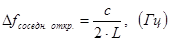, (12)

где 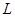- расстояние между отражающими стенками (зеркалами), измеренное по оптической оси, м ( 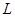заменило размер 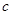закрытого резонатора, ).

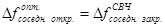4.7. Добротность открытого резонатора

Из общего энергетического определения добротности

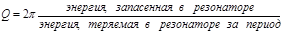(13)

вытекает частная форма записи:

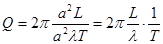(14)

где

- длина волны колебаний в резонаторе, м;

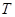- коэффициент пропускания выходного зеркала.

Выражение (14) справедливо для резонатора, заполненного средой без потерь. Из двух зеркал одно – идеальное (коэффициент отражения 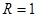), другое – с коэффициентом пропускания 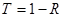. Следовательно,

. (15)

4.8. Угловой сектор, вмещающий высокодобротные типы колебаний, поток энергии которых распространяется под малыми углами к оси резонатора

Если высокодобротными считать колебания, движущиеся наклонно к оси резонатора, добротность которых не более, чем вдвое, уменьшается по сравнению с добротностью колебаний, перемещающихся вдоль оси, то в их число попадают те, которые прежде чем покинуть резонатор, ( 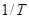) раз отражаются от зеркал. Тогда плоский угол, в пределах которого будут заключены траектории подобных колебаний, равен

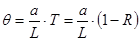. (16)

Соответствующий ему телесный угол равен

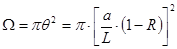. (17)

4.9. Степень разрежения спектра собственных колебаний в открытом резонаторе по сравнению с закрытым

Эффективность разрежения спектра колебаний при переходе от закрытого резонатора к открытому можно оценить той долей, которую составляют высокодобротные колебания открытого резонатора в полном числе колебаний закрытого резонатора. Очевидно, что эта доля определяется отношением 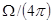, поэтому спектр открытого резонатора разрежается в 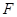раз, где

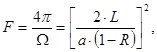(18)

а число типов колебаний (высокодобротных) в полосе 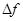около частоты 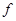для открытого резонатора объемом 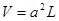с учетом (9) равно

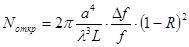. (19)

4.10. Количество зон Френеля, укладывающихся на зеркалах открытого резонатора.

Если квадратные зеркала ( 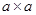) заменить круглыми диаметром 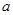, то числом Френеля называют величину

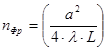. (20)

4.11. Условие частичного разрешения соседних типов колебаний открытого резонатора.

Разрешение двух соседних типов колебаний возможно при неперекрытии их резонансных кривых на оси частот, то есть если

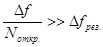. (21)

С учетом (19), (4) и (15) условие (21) приводится к виду

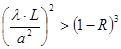. (22)

Выражение (22) справедливо для квадратных зеркал. Если в резонаторе применяются круглые зеркала диаметром 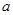, то вместо (22) следует использовать выражение

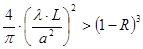, (23)

или, учитывая (20),

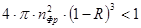. (24)

4.12. Плотность внутрирезонаторного потока энергии колебательной моды.

Если погонное затухание колебания (моды), распространяющегося вдоль оси резонатора, обозначить 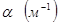, то изменение плотности потока мощности излучения внутри резонатора 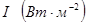подчиняется экспоненциальному закону

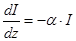. (25)

Безразмерная величина 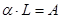определяет полные потери излучения на один проход резонатора, включающие в общем случае потери во внутрирезонаторной среде, в зеркале (на тепло и на прохождение сквозь него), на выход из резонатора через боковую поверхность (дифракционные потери). Тогда для плотности энергии 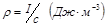уравнение (25) с учетом того, что 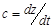, принимает вид

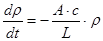. (26)

Его решение

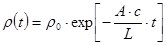(27)

свидетельствует об экспоненциальном затухании с течением времени энергии 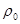собственного колебания, запасенной в начальный момент.

4.13. Время жизни фотона в моде.

Величина

(28)

называется эффективным временем жизни фотона в моде.

Так как

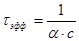, (29)

то, чем больше затухание энергии моды, тем меньшее время проводит фотон в резонаторе перед тем, как перевести свою энергию в тепловую форму или покинуть объем резонатора через боковую поверхность.

Очевидно, что между эффективным временем жизни фотона 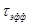и добротностью резонатора имеется взаимосвязь. Возвращаясь к (13),

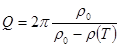, (30)

где

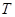- период данного типа колебаний.

Поскольку 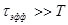, из (30)

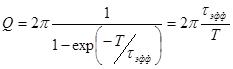. (31)

Для каждого вида потерь характерно свое эффективное время жизни фотона. Поэтому

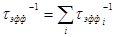. (32)

4.14. Дифракционные потери излучения в открытом резонаторе.

Принципиальное отличие дифракционных потерь от других потерь в среде, заполняющей резонатор, и в зеркалах, состоит в их неустранимости. Приближенная оценка величины дифракционных потерь может быть проведена следующим образом. Допустим, что одно из зеркал освещено равномерно по всей поверхности. Пучок света, движущийся от него в сторону противоположного зеркала, увеличит свой радиус за счет дифракции на . Так как 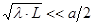, то относительная доля дифракционных потерь определяется чисто геометрически

(33)

или

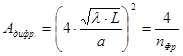. (34)

В действительности распределение амплитуды оптического поля по поверхности зеркала имеет сильно неоднородный характер: например, для низшего типа колебаний – максимум в центре зеркала и плавное уменьшение до нуля к краю. Поэтому реальные потери из-за дифракции на кромке зеркал значительно меньше величины, определяемой выражением (34), и могут быть вычислены с помощью приближенной функции

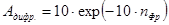. (35)

4.15. Устойчивость открытого резонатора.

По критерию устойчивости открытые резонаторы делятся на три группы: устойчивые, неустойчивые и пограничные. В устойчивых резонаторах оптическое излучение собственного колебания движется следующим образом: оптическое поле со скоростью света перемещается от зеркала к зеркалу под малым углом к оси резонатора и медленно смещается в поперечном направлении. Однако, достигнув каустической поверхности, излучение отражается назад к оси резонатора. Таким образом, в устойчивом резонаторе поток оптической мощности имеет замкнутую траекторию движения и многократно ее повторяет, прежде чем окончательно затухает. В неустойчивом резонаторе поток мощности, достигнув при поперечном смещении открытой боковой поверхности, не отражается назад к оси резонатора, а покидает его, то есть его траектория незамкнута. Резонаторы пограничного типа теряют свою устойчивость при малейшем нарушении их геометрии.

Условие устойчивости открытого резонатора определяется следующим неравенством

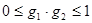, (36)

где

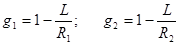, (37)

где 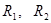- радиусы кривизны зеркал.

Границы области устойчивости (рис. 8) описываются уравнениями:

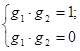. (38)

Рис. 8. Границы устойчивости открытого резонатора (заштрихованы).

5. Указания по технике безопасности

Во время проведения вычислений и компьютерных экспериментов удерживать глаза на расстоянии 0.6 м и более от экрана дисплея.

6. Лабораторное задание и методические указания по его выполнению.

6.1. По п. 4.1., пользуясь (7), рассчитать Q(f) закрытого металлического резонатора в СВЧ диапазоне (f=3•10⁹…3•10¹¹ Гц) и в оптическом диапазоне (f=3•10¹³…3•10¹⁵ Гц), для трех значений σ: σ₁=5,08•10⁷ См/м (медь); σ₂=3,54•10⁷ См/м (алюминий) и σ₃=6,14•10⁷ См/м (серебро). Изобразить графически зависимости Q₁(f), Q₂(f), Q₃(f). Принять μ_а=μ₀=4π•10^-7 Гн/м.

6.2. По п. 4.2, пользуясь (8), рассчитать и построить графически зависимости Δf_рез(f) для тех же условий, что и в п. 6.1.

6.3. По п. 4.3., пользуясь (9), вычислить и построить графически зависимость N_f(f), изменяя f от 3•10⁹ до 3•10¹⁵ Гц.

6.4. По п. 4.4, пользуясь (10), вычислить и построить графически зависимость S_f(f), изменяя f от 3•10⁹ Гц до 3•10¹⁵ Гц. Размер а принять равным: а₁=1 см, а₂=10 см.

6.5. По п. 4.5, пользуясь (11), вычислить и построить графически зависимости Δf_{соседн. закр} (f) для условий, указанных в п. 6.4.

6.6. По п. 4.6, пользуясь (12), вычислить и построить графически зависимость Δf_{соседн. закр} (L), изменяя L в диапазоне от 100 мкм (в полупроводниковом лазере) до 10 м (в лазере на углекислом газе).

6.7. По п. 4.7, пользуясь (15), рассчитать Q для различных типов лазеров. Полупроводниковый лазер: L=100 мкм; λ=0,9 мкм; R₁=0,5 м; R₂=0,75 м. Гелий-неоновый лазер: L=0,1…1 м; λ=0,63 мкм; R₁=0,9 м; R₂=0,95 м; R₃=0,98 м. Лазер на неодиме: L=0,05…1 м; λ=1,06 мкм; R₁=0,86 м; R₂=0,9 м; R₁=0,95 м.

6.8. По п. 4.8, пользуясь (17), рассчитать зависимость Ω(а/L) для следующих значений R: R₁=0,75 м; R₂=0,9 м, R3=0,98 м. Отношение a/L изменять в диапазоне от 50 до 5•10⁵.

6.9. По п. 4.9, пользуясь (18), вычислить и изобразить графически зависимость F(a/L) для условий, принятых в п. 6.8.

6.10. По п. 4.10, пользуясь (20), рассчитать и изобразить графически зависимость n_фр(а/L) для следующих лазеров: полупроводниковый: a₁=1Ч4 мкм²; a₂=1Ч10 мкм²; a₃=1Ч50 мкм²; L=50…100 мкм; λ=0,9 мкм; рубиновый лазер: а₁=3 мм; а₂=9 мм; а₃=12 мм; L=0,05…0,4 м; λ=0,69 мкм; гелий-неоновый лазер: а₁=5 мм; а₂=15 мм; а₃=50 мм; L=0,1…1 м и L=4•10⁴ м; λ=0,63 мкм; углекислотный лазер: а₁=20 мм; а₂=50 мм; а₃=80 мм; L=0,1…10 м; λ=10,6 мкм; дисковый углекислотный лазер: а=100 мм; L=5 мм; λ=10,6 мкм.

6.11. По п. 4.11, пользуясь (14), (23), для лазеров и их параметров, приведенных в п. 6.10, выяснить выполнение условия разрешения при R₁=0,5 м; R₂=0,8 м; R₃=0,95 м.

6.12. По п. 4.13, пользуясь (29), вычислить τ_эфф для резонаторов с затуханием при α₁=0,001; α₂=0,01; α₃=0,1.

6.13. По п. 4.14, пользуясь (35), вычислить A_дифр для лазеров и их параметров, указанных в п. 6.10.

6.14. По п. 4.15, пользуясь (36), (37), выяснить устойчивость следующих открытых резонаторов: L=1м = const.

а) R₁=R₂=∞; е) R₁=R₂=0,25 м;

б) R₁=R₂=10 м; ж) R₁=R₂=-10 м;

в) R₁=R₂=1 м; з) R₁=R₂=-1 м;

г) R₁=R₂=0,75 м; и) R₁= -0,75 м; R₂=0,75 м;

д) R₁=R₂=0,5 м; к) R₁= 0,5 м; R₂=-0,5 м;.

Построить диаграмму g₂(g₁) и отметить на ней точками приведенные варианты резонаторов. Изобразить схематично данные резонаторы, указав на рисунках место положения центров кривизны и их фокусы.

7. Контрольные вопросы для самоподготовки и защиты лабораторной работы.

7.1. Какие типы резонаторов обычно используются в СВЧ диапазоне?

7.2. От чего зависит добротность полого металлического резонатора?

7.3. Какие характеристики закрытого резонатора ухудшаются при уменьшении его добротности?

7.4. Почему закрытый металлический резонатор малых размеров (a ≈ λ) не может быть использован в оптическом диапазоне?

7.5. Почему закрытый металлический резонатор больших размеров (a >> λ) не может быть использован в оптическом диапазоне?

7.6. Почему в открытом резонаторе спектр собственных колебаний значительно разрежен по сравнению с закрытым резонатором?

7.7. Перечислить основные параметры открытых резонаторов. Пояснить их физический смысл.

7.8. Как изменяется с ростом частоты добротность закрытого металлического резонатора фиксированных размеров? При этих же условиях изменяется ли ширина резонансной кривой собственных типов колебаний?

7.9. При условиях п. 7.8 как изменяется частотный «зазор» между соседними колебаниями закрытого резонатора?

7.10. Какой интервал частот разделяет два соседних продольных типа колебаний открытого резонатора? Изменяется ли он с возрастанием частоты?

7.11. Какие виды потерь определяют добротность открытого резонатора?

7.12. Почему дифракционные потери неустранимы принципиально? Как можно уменьшить эти потери?

7.13. Пояснить сущность понятия «зоны Френеля».

7.14. От чего зависит число зон Френеля, укладывающихся на поверхности зеркала открытого резонатора?

7.15. Что определяет продолжительность «жизни фотона» в открытом резонаторе?

7.16. Дать общее определение устойчивых и неустойчивых открытых резонаторов.

7.17. Привести математическую запись критерия устойчивости открытого резонатора.

Список литературы

1. Карлов Н. В. Лекции по квантовой электронике. Учебное пособие для вузов. М.: Наука. 1983. 320 с.

2. Звелто О. Принципы лазеров. М.: Мир. 1990. 560 с.

Дата добавления: 2014-11-08; просмотров: 770; Нарушение авторских прав

Мы поможем в написании ваших работ!