Нагруженные графы

Большинство задач рассматриваемых с применением графов требуют моделей, в которых у каждого ребра необходимо учитывать одно или несколько свойств. Приписывание каждому ребру графа некоего свойства, имеющего одинаковый для всех ребер семантический смысл, называется взвешиванием графа. Значение этого свойства для каждого из ребер (постоянное или получаемого выполнением некоего определенного функционала) называется весом ребра.

В качестве примера рассмотрим транспортную задачу (Рисунок 2.1‑4), в которой объекту находящемуся в вершине v1 требуется за минимальное время достичь вершины v6.

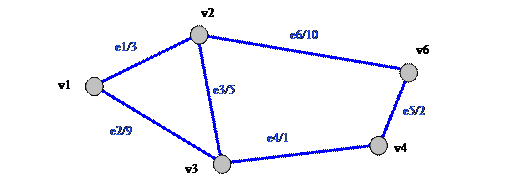
Рисунок 2.1‑4. Пример нагруженного графа

Задачу невозможно решить не зная время, за которое объект в состоянии преодолевать каждое из ребер графа. Доопределим исходные данные и зададим в качестве веса время преодоления ребра. На графе назначенные веса приведены рядом с каждым из ребер через символ “/”, так e3/5 означает что ребро e3 преодолевается за 5, предположим, минут. Теперь, после некоторого размышления, перебрав все четыре возможные пути из v1 в v6, можно сказать что кратчайшим (по времени) способом передвижения из v1 в v6 является путь Pmin(v1,v6)={e1,e3,e4,e5}.

Если немного усложнить только что рассмотренную задачу и требовать определения оптимального по времени маршрута для произвольного объекта с известной скоростью, то очевидно что в графовой модели придется заменить вес – время преодоления ребра на вес – длина ребра (например, в километрах), т.к. каждый из объектов будет проходить ребра за разное время. На той же топологии (отношениях между вершинами) графа, используя другое свойства ребра (другой вес) мы получим уже отличную от первой модель.

Часто используют назначение нескольких весов. Так, если в предыдущей задаче учитывать наличие светофоров и считать что каждый светофор на маршруте удлиняет его, скажем на 1 минуту, то придется использовать модель с двумя весами, первым из которых будет длина ребра, а вторым – количество светофоров.

Дата добавления: 2014-11-15; просмотров: 395; Нарушение авторских прав

Мы поможем в написании ваших работ!