СТАЦИОНАРНОЕ ЭЛЕКТРОМАГНИТНОЕ ПОЛЕ

1. Запишите закон Ома для однородного участка цепи. Немецкий физик Г. Ом в 1826 году экспериментально установил, что сила тока I, текущего по однородному металлическому проводнику, пропорциональна напряжению U на концах проводника: 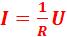, где R = const. Это соотношение выражает закон Ома для однородного участка цепи: сила тока, текущего по однородному (в смысле отсутствия сторонних сил) металлическому проводнику, пропорциональна падению напряжения U на проводнике. Величину R принято называть электрическим сопротивлением.

2. Что такое электрический ток. Электрическим током называется упорядоченное движение электрических зарядов. За направление тока принимают направление движения положительных зарядов, которое противоположно направлению движения отрицательных зарядов. Различают: ток проводимости (ток в проводниках), конвекционный ток и ток в вакууме.

3. Назовите характеристики электрического тока и их единицы измерения. Количественной характеристикой электрического тока служит сила тока I –скалярная физическая величина, равная отношению заряда dq, переносимого через поперечное сечение проводника за интервал времени dt, к этому интервалу времени: 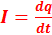.В международной системе единиц СИ сила тока измеряется в амперах (А).

В качестве характеристики, задающей распределение силы тока по поперечному сечению проводника служит вектор плотности тока 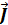. Плотностью электрического тока называется вектор 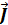, совпадающий с направлением электрического тока в рассматриваемой точке и численно равный отношению силы тока dI сквозь малый элемент поверхности, перпендикулярной направлению тока, к площади dS_⊥ этого элемента: 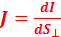. Единицей измерения плотности тока является А/м².

4. Назовите условия, выполнение которых необходимо для протекания в цепи электрического тока. Условия, необходимые для проявления и существования электрического тока проводимости в среде: а) наличие в среде свободных носителей заряда, т.е. заряженных частиц, способных перемещаться. В металле это электроны проводимости; в электролитах – положительные и отрицательные ионы; в газах – положительные, отрицательные ионы и электроны. б) наличие в среде электрического поля, энергия которого затрачивалась бы на перемещение электрических зарядов. Для того, чтобы ток был длительным, энергия электрического поля должна все время пополняться, т.е. нужен источник электрической энергии – устройство, в котором происходит преобразование какого-либо вида энергии в энергию электрического тока.

5. Какие силы по своей природе не могут быть сторонними. Если в цепи на носители тока действуют только силы электростатического поля (кулоновские), то происходит перемещение носителей (они предполагаются положительными) от точек с большим потенциалом к точкам с меньшим потенциалом. Это приведет к выравниванию потенциалов во всех точках цепи и к исчезновению электрического поля. Поэтому для существования постоянного тока необходимо наличие в цепи устройства, способ­ного создавать и поддерживать разность потенциалов за счет работы сил не электростатического происхождения. Такие устройства называются источниками тока. Силы не электростатического происхождения, действующие на заряды со стороны источников тока, называются сторонними. Эти силы могут быть обусловлены химическими процессами, диффузией носителей тока в неоднородной среде или через границу двух разнородных веществ, электрическими полями, порождаемыми меняющимся во времени магнитным полем.

6. Чему равна циркуляция вектора напряженности сторонних сил. Вне источника напряженность поля сторонних сил отсутствует, т.е. равна нулю, поэтому при перемещении положительного заряда по замкнутой цепи работу сторонних сил можно представить как интеграл по всему замкнутому контуру 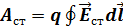( 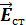– напряженность поля сторонних сил, определяемая сторонней силой, действующей на единичный положительный заряд внутри источника). Отсюда ЭДС, действующая в замкнутой цепи - циркуляция вектора напряженности поля сторонних сил: 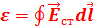. Если цепь разомкнута, то ЭДС останется по величине такой же, поскольку определяется только на промежутке источника тока.

7. Запишите обобщенный закон Ома (закон Ома для неоднородного участка цепи). Для неоднородного участка цепи (участка, содержащего ЭДС), закон Ома записывается в следующей форме: . Это соотношение принято называть обобщенным законом Ома. Обобщенный закон Ома выражает закон сохранения энергии применительно к участку цепи постоянного тока. Он в равной мере справедлив как для пассивных участков (не содержащих ЭДС), так и для активных.

8. Запишите закон Ома для замкнутой цепи. Закон Ома для замкнутой цепи, содержащей источник ЭДС, запишется в виде: 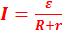. Эта формула выражает закон Ома для полной цепи: Сила тока в полной цепи равна электродвижущей силе источника, деленной на сумму сопротивлений однородного и неоднородного участков цепи.

9. Сформулируйте и запишите формулу закона Джоуля-Ленца (в интегральной или дифференциальной форме). Независимо друг от друга Джоуль и Ленца показали, что при протекании тока, в проводнике выделяется количество теплоты: 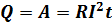(работа электрического тока, протекающего по неподвижному проводнику с сопротивлением, преобразуется в тепло, выделяющееся на проводнике).Если ток изменяется со временем, то 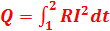. Это закон Джоуля-Ленца в интегральной форме. Отсюда видно, что нагревание происходит за счет работы, совершаемой силами поля над зарядом.

Закон Джоуля-Ленца в дифференциальной форме выражен следующей формулой: 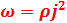(удельная тепловая мощность тока пропорциональна квадрату плотности электрического тока и удельному сопротивлению среды в данной точке).

Приведенные формулы справедливы для однородного участка цепи и для неоднородного при условии, что действующие в них сторонние силы имеют нехимическое происхождение.

10. Дайте определение вектора магнитной индукции, назовите ее размерность и приведите соответствующие формулы (через силу Ампера и через вращающийся момент). Вектор магнитной индукции — векторная физическая величина, являющаяся силовой характеристикой магнитного поля в данной точке пространства. Вектор магнитной индукции определяет силы, действующие на токи или движущиеся заряды в магнитном поле. В СИ единицей измерения магнитной индукции является тесла: 1 Тл = Дж/А·м² = Н·м/А·м² = Н/А·м Силовое действие магнитного поля может обнаруживаться по действию силы Ампера на прямолинейный проводник с током и по вращающемуся действию на замкнутый контур. При исследовании магнитного поля с помощью прямолинейного проводника с током магнитная индукция определяется следующим образом: модуль магнитной индукции равен отношению максимального значения модуля силы Ампера F, действующий на проводник с током, к силе тока I в проводнике и его длине l: 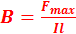. При исследовании магнитного поля с помощью контура с током магнитная индукция определяется следующим образом: модуль вектора индукции равен отношению максимального вращающегося момента сил М, действующего на рамку с током со стороны магнитного поля, к произведению силы тока I в рамке на ее площадь S: .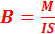

11. Что называется магнитным моментом контура с током. (приведите соответствующий момент). Магнитный момент контура с током (магнитный дипольный момент) — основная векторная величина, характеризующая магнитные свойства вещества: 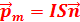,где I - сила тока в контуре, S - площадь поверхности контура (рамки), 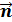- единичный вектор нормали к поверхности рамки. Направление вектора 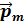совпадает с направлением положительной нормали к контуру.

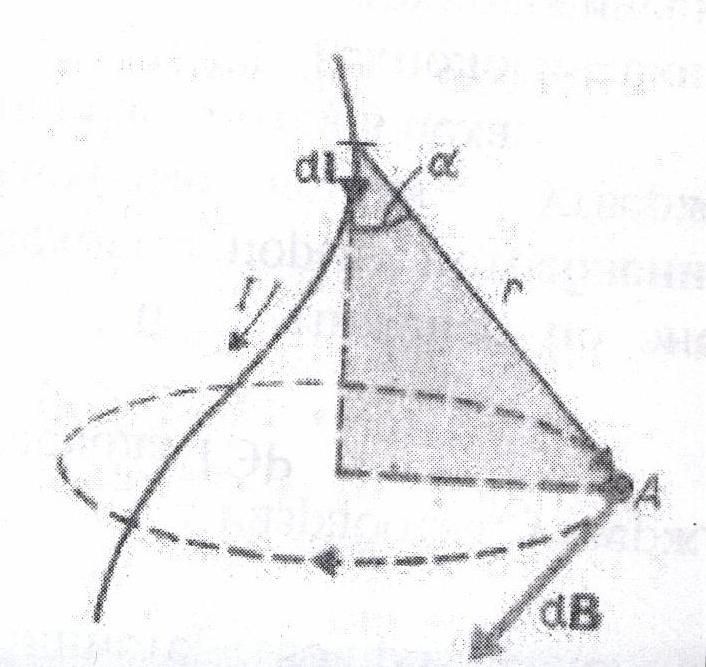
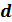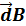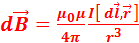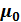12. Запишите закон Био-Савара-Лапласа (формула и расшифровка всех величин, входящих в нее, привести рисунок). Закон Био — Савара — Лапласа для проводника с током I, элемент которого l создает в некоторой точке А индукцию поля , записывается в виде , где - магнитная постоянная, d 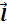- вектор, по модулю равный длине dl элемента проводника и совпадающий по направлению с током, 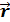- радиус-вектор, проведенный из элемента d 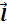проводника в точку А поля, r — модуль радиуса-векто­ра 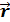. Направление d перпендикулярно d 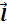и r, т. е. перпендикулярно плоскости, в ко­торой они лежат, и совпадает с каса­тельной к линии магнитной индукции. Это направление может быть найдено по пра­вилу нахождения линий магнитной индук­ции (правилу правого винта): направле­ние вращения головки винта дает направ­ление d , если поступательное движение винта соответствует направлению тока в элементе.

13. Приведите формулировку и математическую запись в интегральной форме закона полного тока (теорема о циркуляции) для магнитного поля в вакууме. Закон полного тока для магнитного поля в вакууме (теорема о циркуляции вектора ): циркуляция вектора по про­извольному замкнутому контуру равна произведению магнитной постоянной m₀ на алгебраическую сумму токов, охватывае­мых этим контуром: 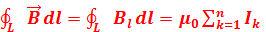, где n — число проводников с токами, ох­ватываемых контуром L произвольной формы. Каждый ток учитывается столько раз, сколько раз он охватывается конту­ром. Положительным считается ток, на­правление которого связано с направлени­ем обхода по контуру правилом правого винта; ток противоположного направления считается отрицательным.

14. Поток вектора магнитной индукции (определение, математическая запись), размерность. Потоком вектора магнитной индукции (магнитным потоком) через площадку dS называется скалярнаяфизическая величи­на, равная dФ_B = 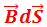= B_n dS , где B_n = Вcosa — проекция вектора на направление нормали к площадке dS (a — угол между векторам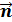и и ), dS = dSn — вектор, модуль которого ра­вен dS, а направление совпадает с направ­лением нормали 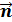к площадке. Поток вектора может быть как положительным, так и отрицательным в зависимости от знака cosa (определяется выбором положительного направления нормали 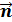). Поток вектора связывают с контуром, по которому течет ток. В таком случае положительное направление нормали к контуру нами уже определено, оно связывается с током правилом правого винта. Таким образом, магнитный поток, создаваемый контуром через поверхность, ограниченную им самим, всегда положителен. Поток вектора магнитной индукции 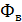через произвольную поверхность S равен 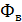= 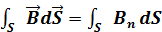Для однородного поля и плоской по­верхности, расположенной перпендикуляр­но вектору , B_n = B = const и 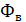= ВS. Из этой формулы определяется единица магнитного потока вебер (Вб): 1 Вб — магнитный поток, проходящий через плоскую поверхность площадью 1 м², рас­положенную перпендикулярно однородно­му магнитному полю, индукция которого равна 1 Тл (1 Вб = 1 Тл·м²).

15. Приведите формулировку и математическую запись в интегральной форме теоремы Остроградского – Гаусса для магнитного поля. Теорема Гаусса для вектора : поток век­тора магнитной индукции через любую замкнутую поверхность равен нулю: 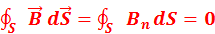Эта теорема отражает факт отсутствия магнитных зарядов, вследствие чего линии магнитной индукции не имеют ни начала, ни конца и являются замкнутыми.

16. Запишите закон Ампера для силы взаимодействия двух параллельных токов. Два параллельных тока одинакового направления притягиваются друг к другу с силой dF = 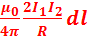Если токи имеют противоположные на­правления, то, используя правило левой руки, можно показать, что между ними действует сила отталкивания, определяе­мая приведенной формулой.

17. Запишите закон Ампера для элемента проводника с током в магнитном поле в векторной форме. Магнитное поле оказывает на рамку с током ориентирующее действие. Следовательно, вращающий момент, испытываемый рамкой, есть результат действия сил на отдельные ее элементы. Обобщая результаты исследования магнитного поля на различные проводники с током, Ампер установил, что сила 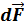, с которой магнитное поле действует на элемент проводника d 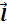с током, находящегося в магнитном поле, равна 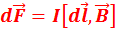, где 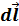– вектор, по модулю равный d 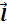и совпадающий по направлению с током, – вектор магнитной индукции. Направление вектора 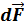может быть найдено по общим правилам векторного произведения, откуда следует правило левой руки: если ладонь левой руки расположить так, чтобы в нее входил вектор , а четыре вытянутых пальца расположить по направлению тока в проводнике, то отогнутый большой палец покажет направление силы, действующей на ток.

18. Запишите выражение для силы Лоренца. Опыт показывает, что магнитное поле действует не только на проводники с током, но и на отдельные заряды, движущиеся в магнитном поле. Сила, действующая на электрический заряд q, движущийся в магнитном поле со скоростью 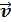, называется силой Лоренца и выражается формулой 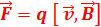, где – индукция магнитного поля, в котором заряд движется. Направление силы Лоренца определяется с помощью правила левой руки: если ладонь левой руки расположить так, чтобы в нее входил вектор , а четыре вытянутых пальца направить вдоль вектора 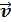(для q > 0 направления 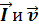совпадают, для q < 0 – противоположны), то отогнутый большой палец покажет направление силы, действующей на положительный заряд.

19. Запишите выражение для работы, которая совершается при перемещении проводника с током в магнитном поле. Работа по перемещению проводника с током в магнитном поле равна произведению силы тока на магнитный поток, пересеченный движущимся проводником: 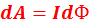. Формула справедлива и для произвольного направления вектора .

20. Запишите выражение для работы, которая совершается при перемещении контура с током в магнитном поле. Работа по перемещению замкнутого контура с током в магнитном поле равна произведению силы тока в контуре на изменение магнитного потока, сцепленного с контуром: 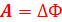. Формула остается справедливой для контура любой формы в произвольном магнитном поле.

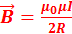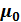21. Запишите выражение для индукции магнитного поля (B) в центре кругового витка с током I и радиусом R. Магнитная индукция поля в центре кругового проводника с током равна , где – магнитная постоянная, μ — магнитная проницаемость среды, в которой находится проводник, I – сила тока в проводнике, R – радиус кругового витка.

22. Запишите выражение для индукции магнитного поля (B), создаваемого прямым бесконечным проводником с током в произвольной точке. Для прямолинейного бесконечно длинного проводника с током симметрия линий напряженности и индукции в изотропной среде позволяет определить величину магнитного поля в любой точке на расстоянии R от оси проводника. Линии напряженности и магнитной индукции поля прямолинейного проводника представляют собой концентрические окружности, лежащие в плоскостях, перпендикулярных проводнику. Вдоль линии напряженность (индукция) магнитного поля одинакова и циркуляция равна произведению напряженности (индукции) на длину линии. 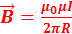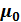Соответственно магнитная индукция поля прямого тока равна , где – магнитная постоянная, μ — магнитная проницаемость среды, в которой находится проводник, I – сила тока в проводнике, R – расстояние до проводника.

23. Что называется вектором намагниченности (J). (формула, размерность). Вещество, помещенное во внешнее магнитное поле, намагничивается. Степень намагничения вещества принято характеризовать вектором намагничения 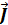. Вектором намагниченности (намагничения) называется физическая величина, численно равная суммарному магнитному моменту единицы объема вещества: 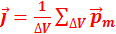, где 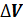– физически бесконечно малый объем, взятый в окрестности рассматриваемой точки, 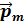– магнитный момент отдельной молекулы. Суммирование производится по всем молекулам, заключенным в объеме 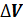. В СИ имеет название ампер на метр и обозначается А/м.

24. Запишите формулу, связывающую магнитную индукцию В в магнетике с магнитной проницаемостью 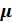и напряженностью магнитного поля Н в этом магнетике. Вектор напряженности магнитного поля является дополнительным вектором к силовому вектору индукции магнитного поля . Векторы и между собой связаны наподобие векторов напряженности электрического поля 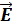и электрического смещения 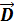. А именно, для од­нородной изотропной среды вектор маг­нитной индукции связан с вектором на­пряженности следующим соотношением: 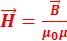, где m₀ — магнитная постоянная, m — без­размерная величина — магнитная прони­цаемость среды, показывающая, во сколь­ко раз магнитное поле макротоков уси­ливается за счет поля микротоков среды. Таким образом, напряженность магнитного поля есть вектор, имеющий то же направление, что и вектор , но в 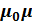раз меньший по модулю (в анизотропных средах векторы и , вообще говоря, не совпадают по направлению).

25. Запишите формулу, связывающую векторы намагниченности и напряженности магнитного поля. Вектор намагниченности принято связывать не с магнитной индукцией, а с напряженностью поля. Вектор намагничения пропорционален напряженности магнитного поля 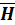, вызывающего намагничени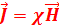е , где 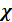– характерная для данного магнетика величина, называемая магнитной восприимчивостью вещества, численно равная величине вектора намагниченности магнетика при напряженности магнитного поля равной единице. Следовательно, магнитная восприимчивость парамагнетиков положительна ( 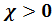), диамагнетиков – отрицательна ( ).

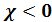26. Сформулируйте закон полного тока (теорема о циркуляции) для магнитного поля в веществе и запишите его математическое выражение в интегральной форме. Теорема о циркуляции вектора магнитной индукции (закон полного тока): циркуляция вектора магнитной индукции по произвольному замкнутому контуру равна произведению магнитной постоянной μ₀ на алгебраическую сумму токов, охватываемых этим контуром: 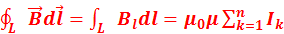,где n — число проводников с токами, которые охватываются контуром L любой формы. Каждый ток в уравнении учитывается столько раз, сколько раз он охватывается контуром. Ток считается положительным, если его направление образует с направлением обхода по контуру правовинтовую систему; отрицательным считается ток противоположного направления. Закон полного тока является интегральной формулировкой закона Био-Савара и входит в систему уравнений Максвелла.

27. Назовите типы магнетиков. В зависимости от знака и величины магнитной восприимчивости все магнетики подразделяются на три группы: 1) диамагнетики, у которых χ отрицательна мала по абсолютной величине ( 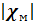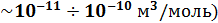; 2) парамагнетики, у которых χ тоже невелика, но положительна (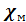 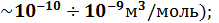3) ферромагнетики, у которых χ положительна и достигает очень больших значений ( 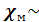1 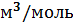). Кроме того, в отличие от диа- и парамагнетиков, для которых χ не зависти от , восприимчивость ферромагнетиков является функцией напряженности магнитного поля.

28. Что называется спином электрона. Существование собственных моментов электрона первоначально пытались объяснить, рассматривая электрон как заряженный шарик, вращающийся вокруг своей оси. В соответствии с этим собственный механический момент электрона получил название СПИН (от англ. to spin – вращаться). Однако вскоре обнаружилось, что такое представление приводит к ряду противоречий, и от гипотезы о «вращающемся» электроне пришлось отказаться. В настоящее время принимается, что собственный механический момент (спин) и связанный с ним собственный (спиновый) магнитный момент являются такими же неотъемлемыми свойствами электрона, как и его масса и заряд. И так, электрон, обладающий собственным механическим моментом импульса 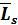, называется спином. Спину электрона соответствует собственный (спиновый) магнитный момент 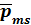. Проекция спина на направление вектора 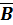может принимать только одно из следующих двух значений 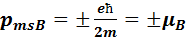, где ħ = 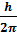( h – постоянная Планка), 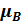– магнетон Бора, являющийся единицей магнитного момента электрона.

29. Приведите закон преломления линий вектора 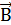на границе раздела двух магнетиков. Вблизи поверхности раздела двух магнетиков векторы и должны удовлетворять определенным граничным условиям, которые вытекают из соотношений 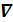B = 0, 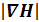= j. В соответствии с тем, что 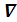B = 0, поток вектора через любую замкнутую поверхность равен нулю. Сосчитаем поток вектора через поверхность малого цилиндра, охватывающего границу раздела 2-х сред: 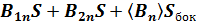=0, где S - площадь основания цилиндра, 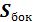- площадь боковой поверхности. Устремляя высоту цилиндра h → 0 и, 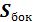→ 0 получаем на границе: 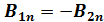и, учитывая, что 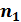и 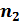- противоположно направленные нормали, и вводя общую нормаль, имеем: Итак: нормальные составляющие вектора непрерывны на границе раздела двух магнетиков.

Дата добавления: 2014-11-24; просмотров: 400; Нарушение авторских прав

Мы поможем в написании ваших работ!