
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Реакция линейной непрерывной системы на стохастическое воздействие стационарное в широком смысле типа непрерывный «белый шум»
Исходные данные
(s) 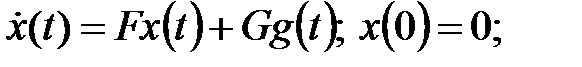
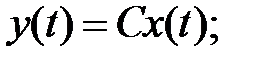
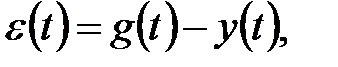
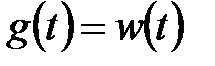 - белый шум:
- белый шум: 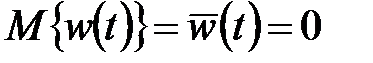 ;
;
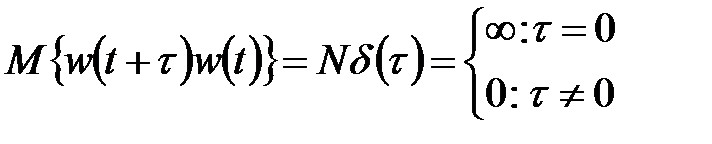 .
.
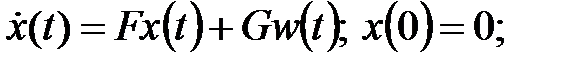
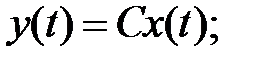
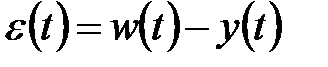 .
.
Найти
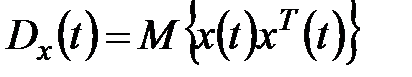 ;
;
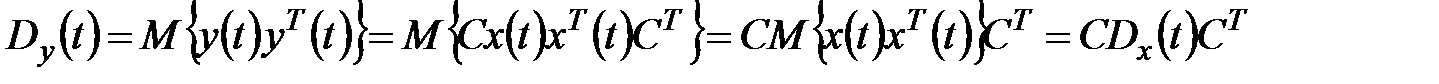 ;
;
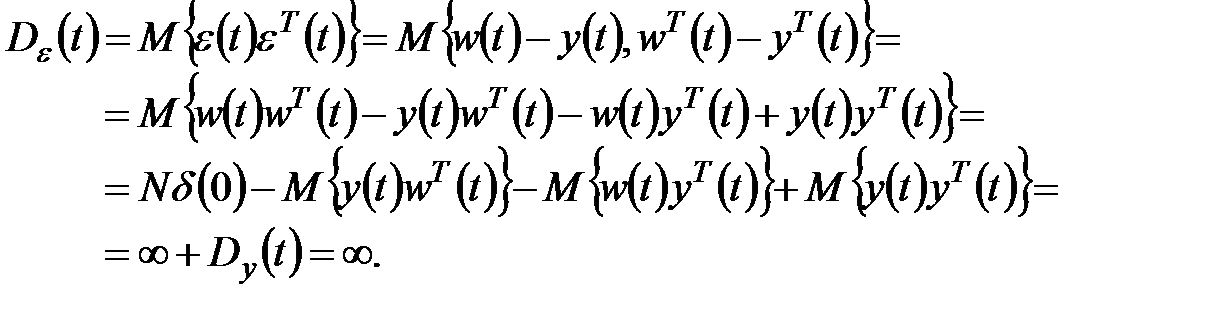
Ранее показано, что
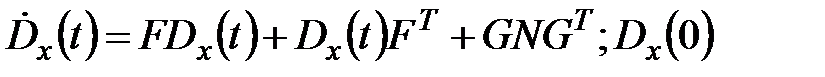
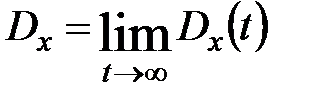 ;
; 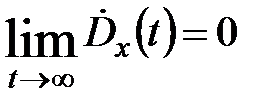
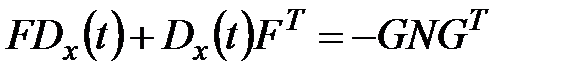
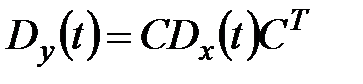
Примеры
Пример 3.1
Рассмотрим в качестве системы формирующий фильтр (ФФ), на выходе которого при 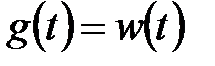 наблюдается окрашенный шум
наблюдается окрашенный шум 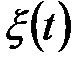 типа «Экспоненциально окрашенный».
типа «Экспоненциально окрашенный».
ФФ: 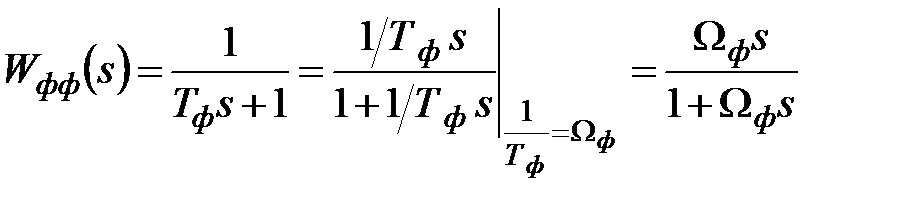
Рисунок 3.1 – Структурное представление ФФ
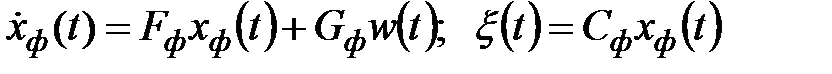
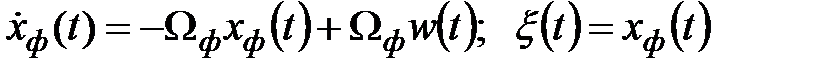
Тогда
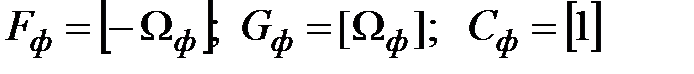
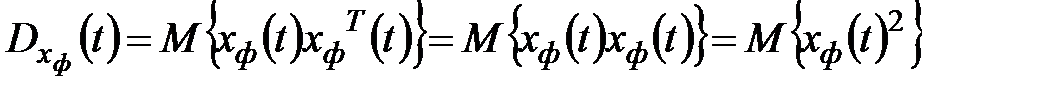 ;
;
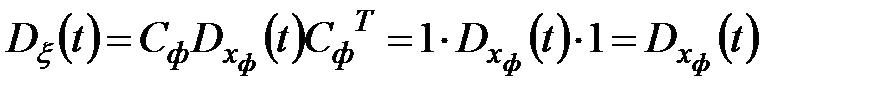 ;
;
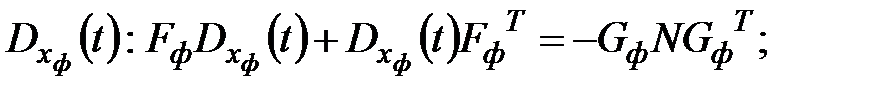
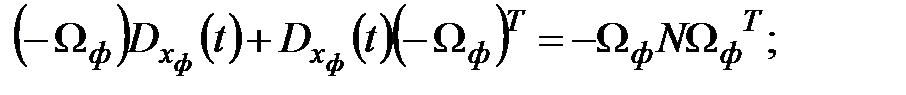
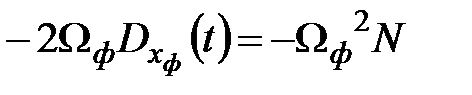 .
.
Итак получим 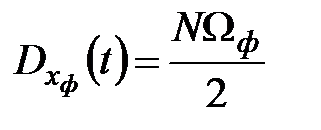 .
.
Оценим физическую размерность интенсивности 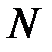 белого шума
белого шума 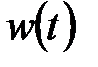
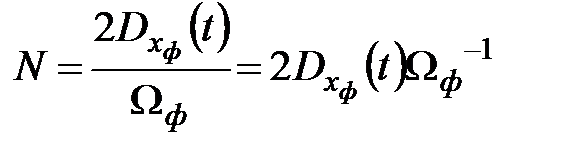
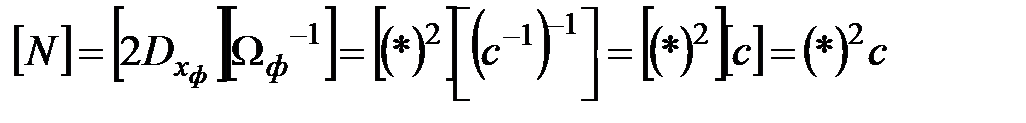 ,
,
где * имеет смысл:
· метра, миллиметра, микрометра при стохастическом процессе типа линейных перемещений;
· радиана, градуса, угловой секунды при стохастическом процессе типа угловых перемещений;
· вольты, милливольты, амперы, миллиамперы при электрических стохастических процессах.
Пример 3.2
Рассмотрим в качестве системы ФФ, на выходе которого при 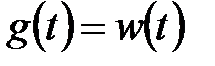 формируется окрашенный шум
формируется окрашенный шум 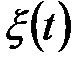 типа «нерегулярная качка». В этом случае
типа «нерегулярная качка». В этом случае
ФФ: 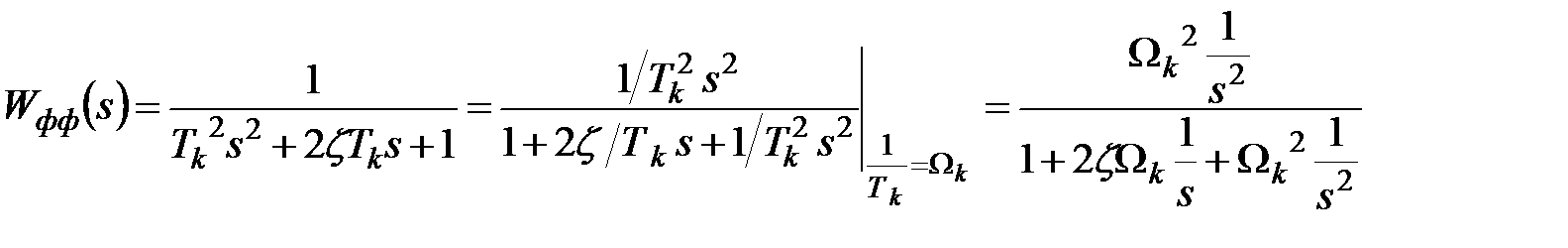
Рисунок 3.2 – Структурное представление ФФ
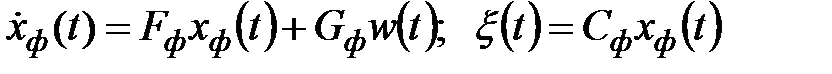 ,
,
где 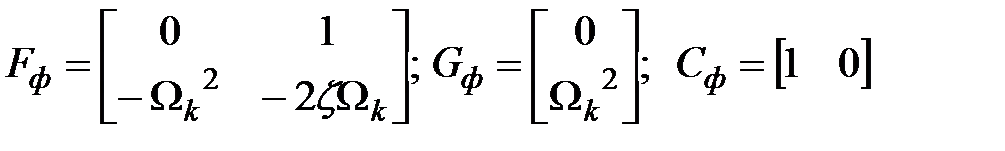 .
.
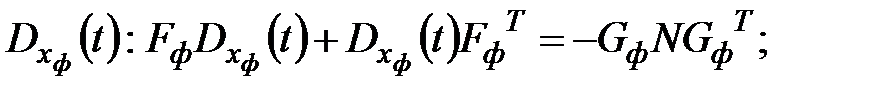
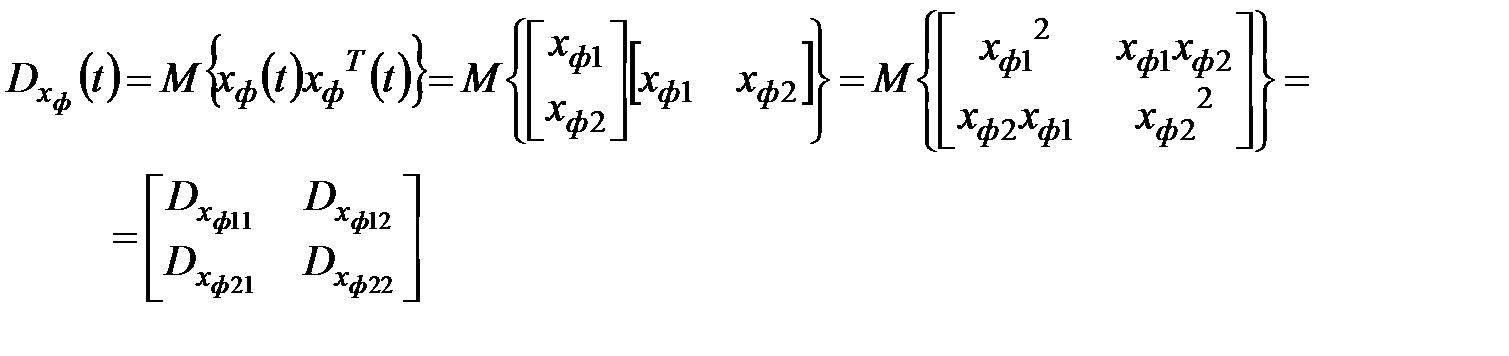
при этом 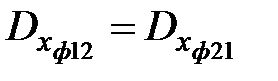 , поэтому в уравнении Ляпунова будем представлять
, поэтому в уравнении Ляпунова будем представлять 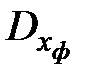 в форме
в форме
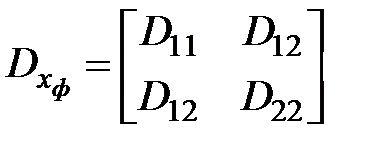 , где
, где 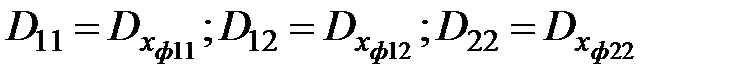 .
.
Тогда получим
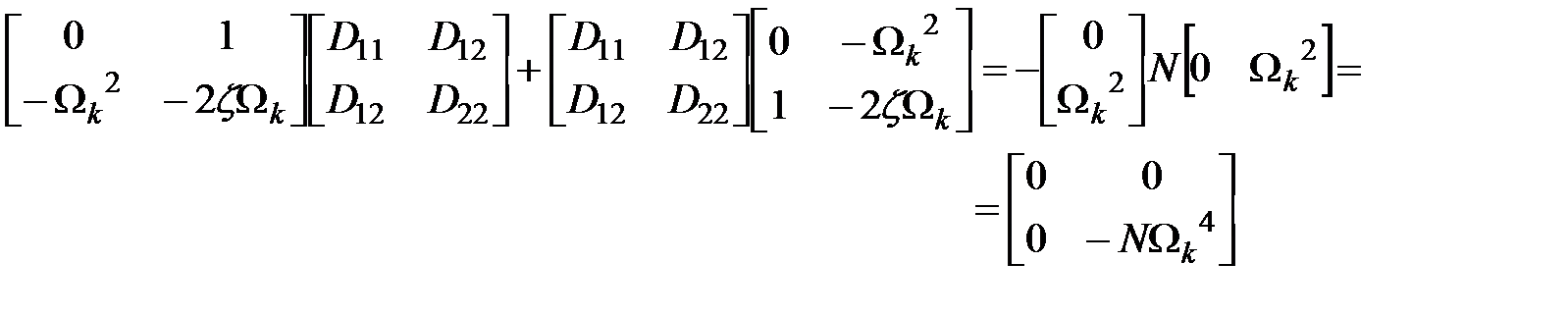
Поэлементное умножение матриц порождает систему равенств
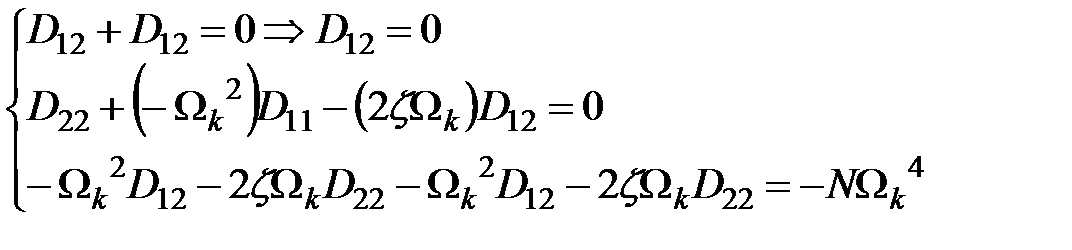
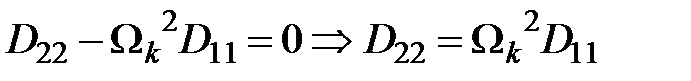
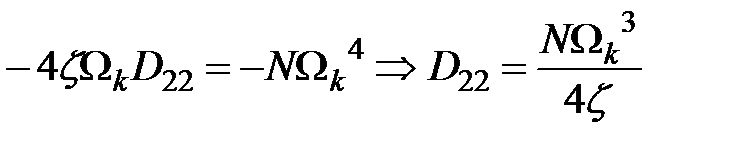
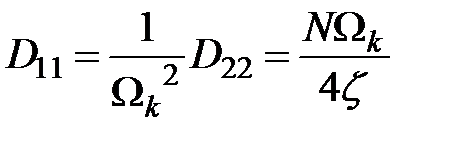
Матрица дисперсий 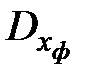 принимает вид
принимает вид
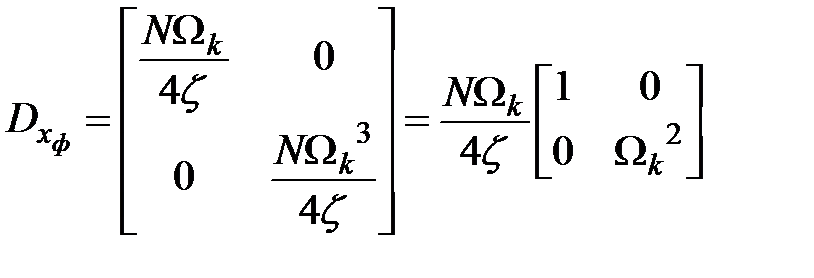 .
.
Дисперсия 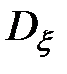 окрашенного шума типа «нерегулярная качка» определится из соотношения
окрашенного шума типа «нерегулярная качка» определится из соотношения
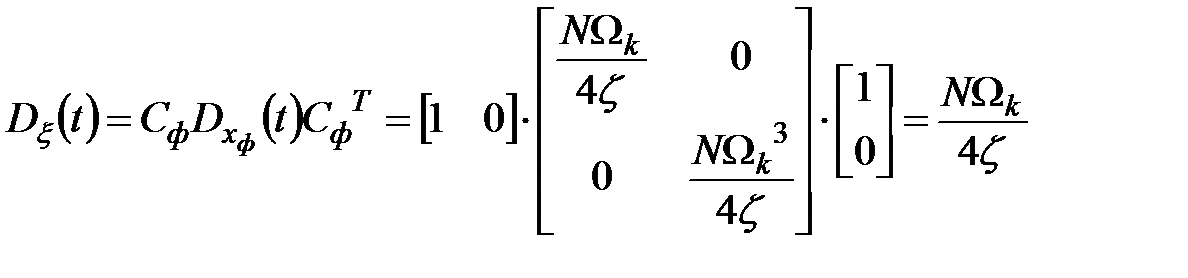 .
.
Итак получим 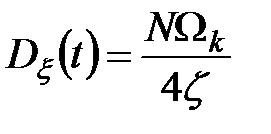 .
.
Тема: Реакция непрерывной линейной системы на стохастическое воздействие типа окрашенный шум
(s) 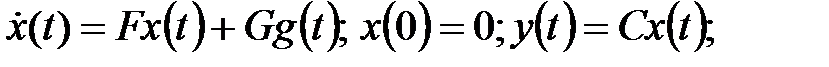
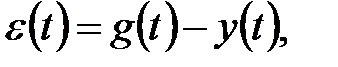
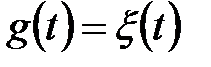
(ФФ) 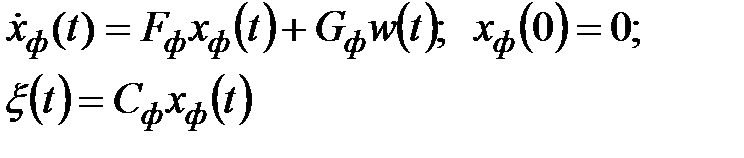
Для сведения задачи к уравнению Ляпунова введем в рассмотрение агрегированную систему с вектором состояния
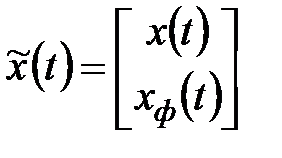 .
.
Тогда объединяя описания (s) и (ФФ) получим
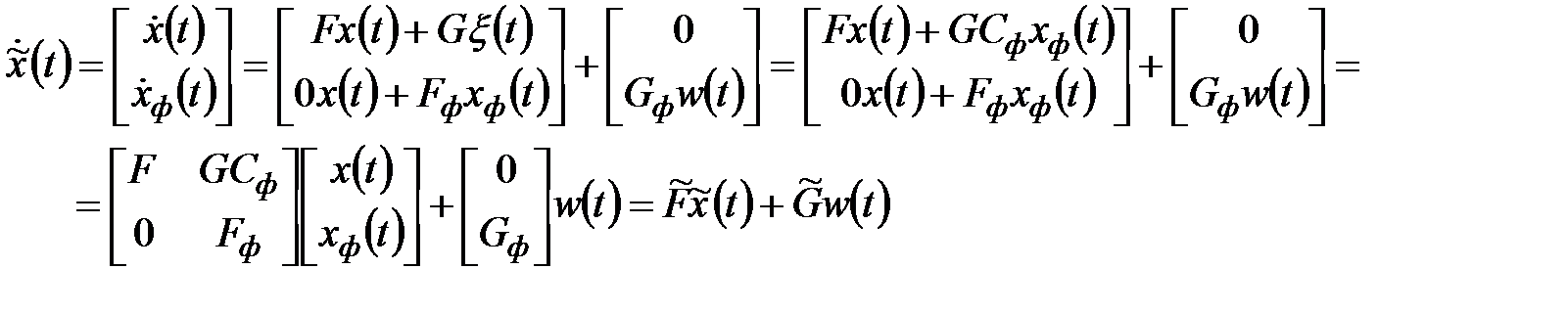 ,
,
где 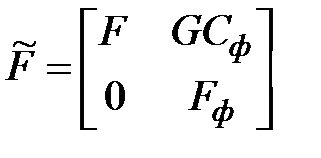 ;
; 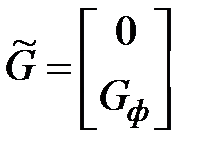 .
.
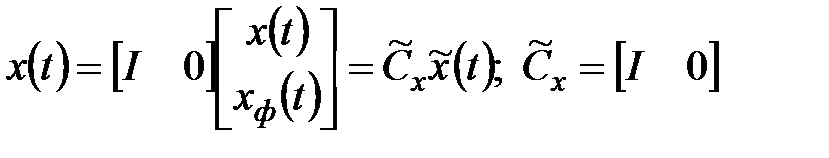 ;
;
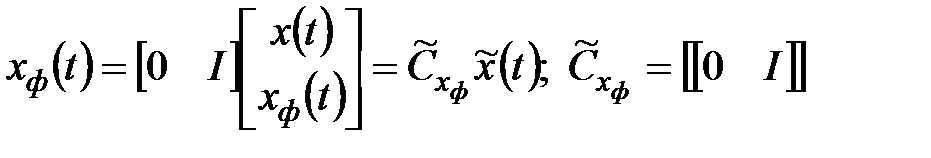 ;
;
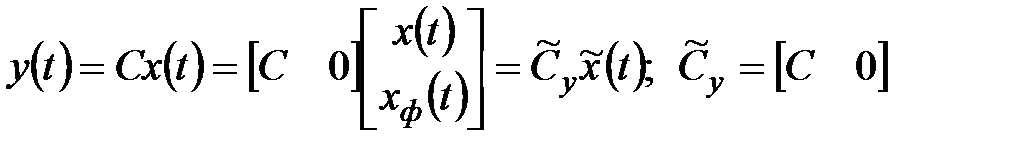 ;
;
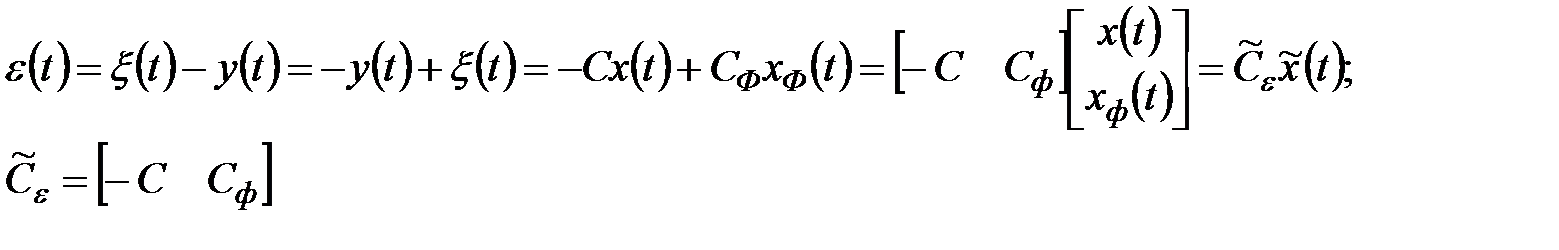
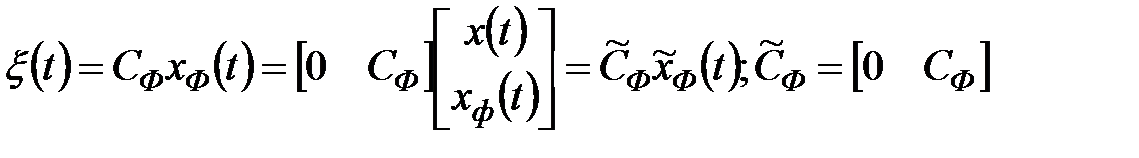 .
.
Очевидно, для агрегированной системы (AS)
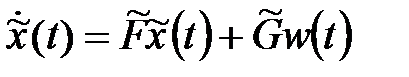
оказывается справедливым использование уравнения Ляпунова
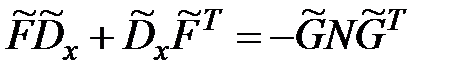 ,
,
где 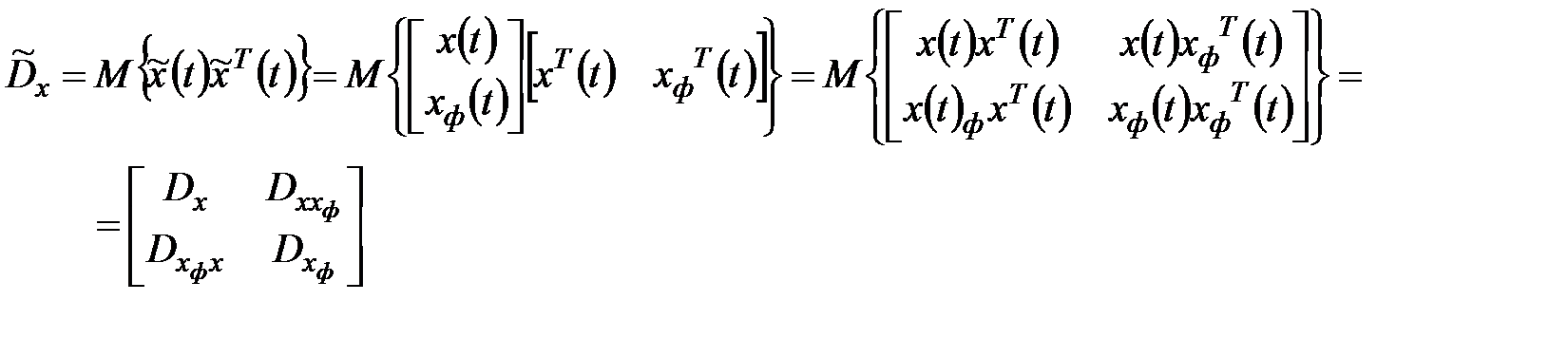
где 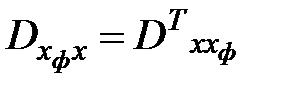 .
.
Тогда для переменных агрегированной системы 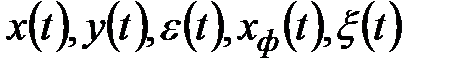 получим представления их матриц дисперсий
получим представления их матриц дисперсий
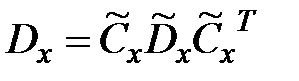 ;
;
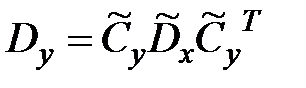 ;
;
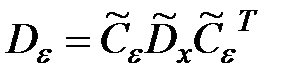 ;
;
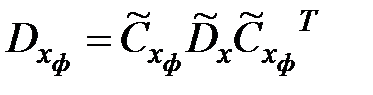 ;
;
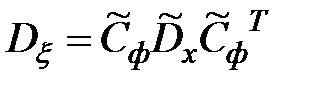 .
.
Разобьем уравнение Ляпунова относительно матрицы 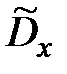 дисперсии агрегированного вектора состояния
дисперсии агрегированного вектора состояния 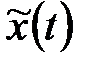 на компоненты, записав его в форме
на компоненты, записав его в форме
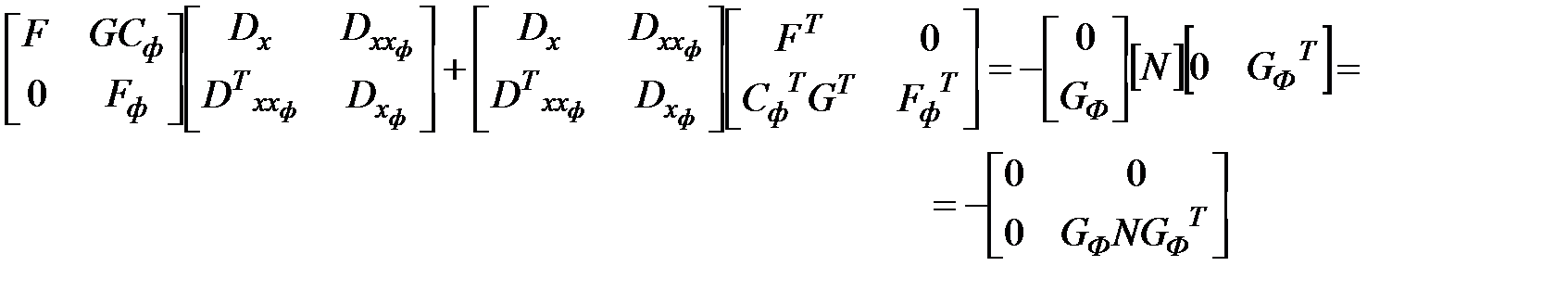
Поэлементное перемножение матриц дает систему уравнений
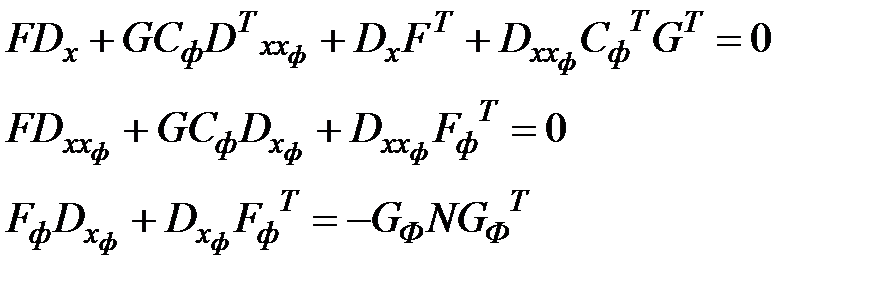
Порядок решения уравнений Ляпунова
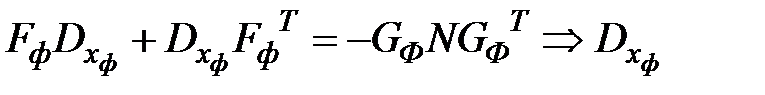
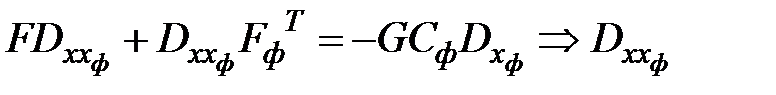
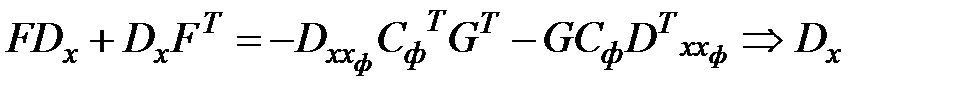 .
.
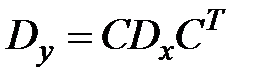 ;
;
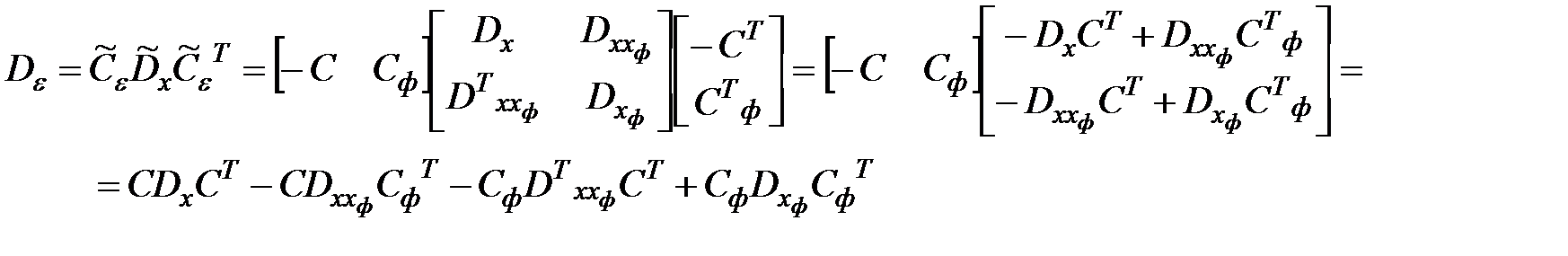 .
.
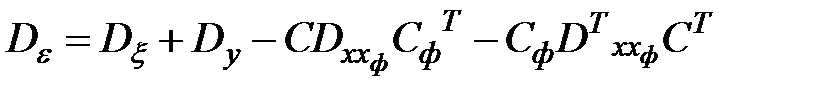
Лекция № 4
Пример 4.1
Рассмотрим систему второго порядка, возбуждаемую стохастическим входным воздействием 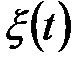 типа «экспоненциально коррелированным окрашенным шумом».
типа «экспоненциально коррелированным окрашенным шумом».
Рисунок 4.1 – Структурное представление задачи
(s) 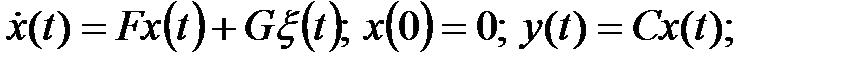
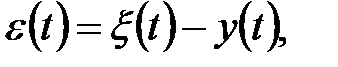
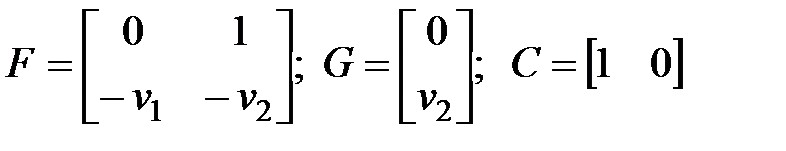
(ФФ) 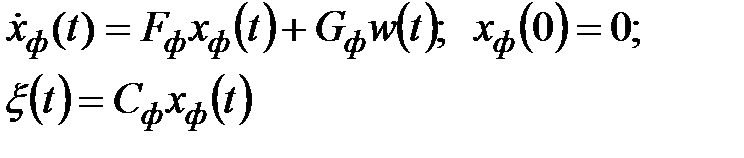
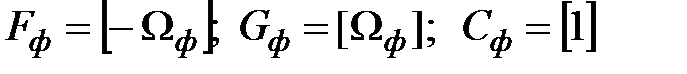
Решение матричного уравнения
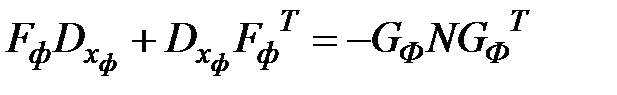
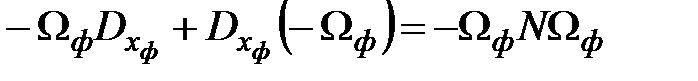
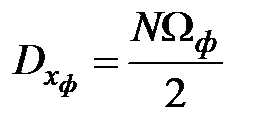
Решение матричного уравнения
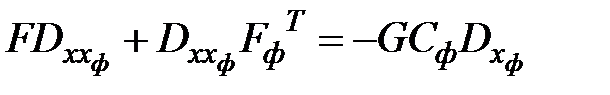
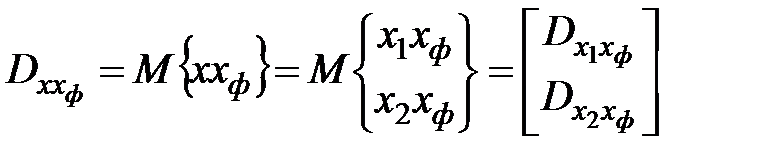
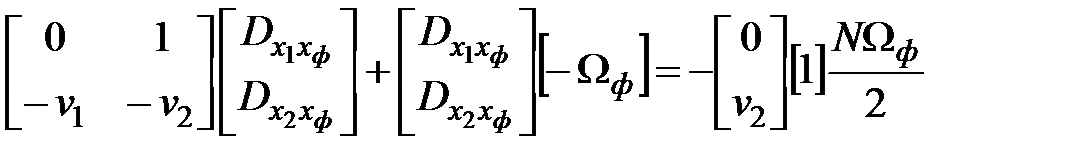
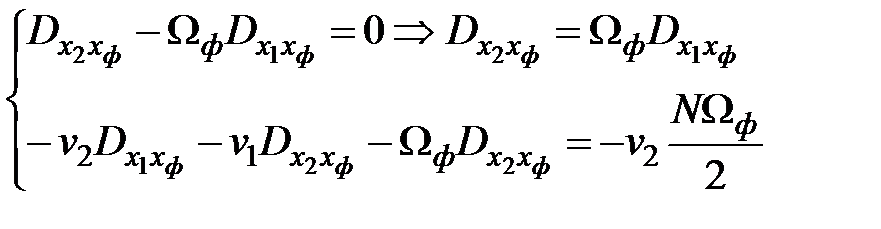
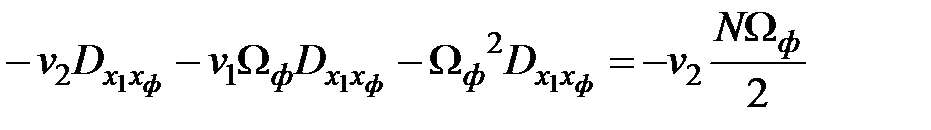
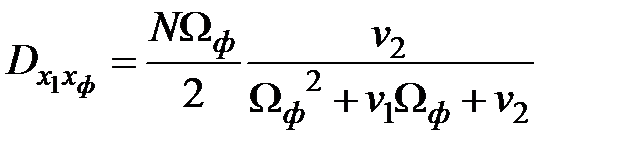 ;
;
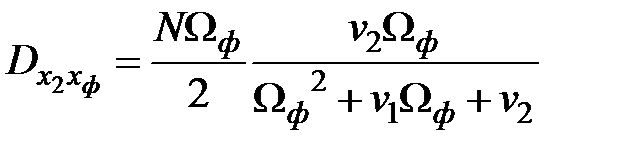
Решение матричного уравнения
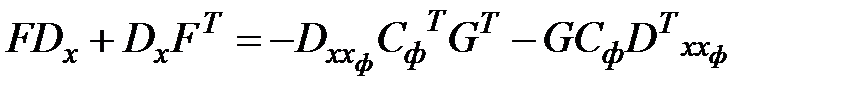
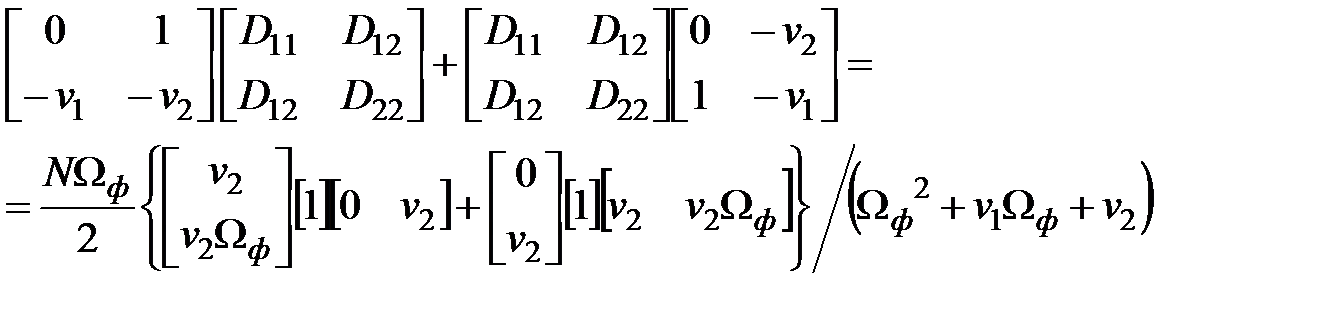
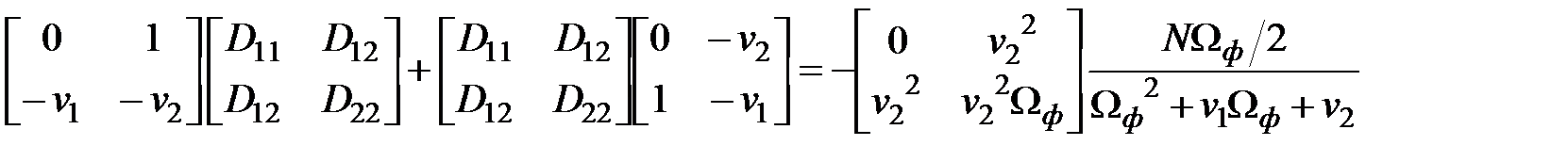
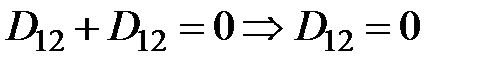 ;
;
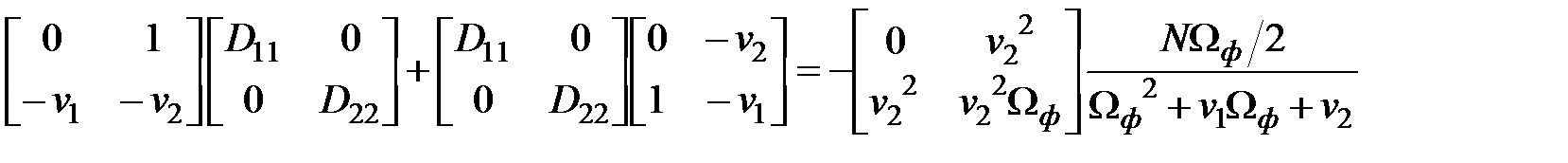
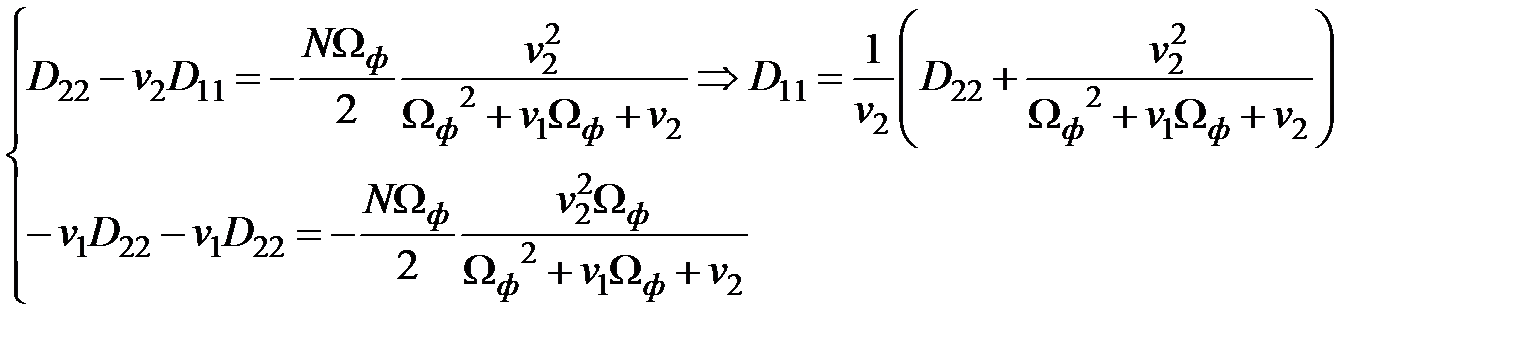
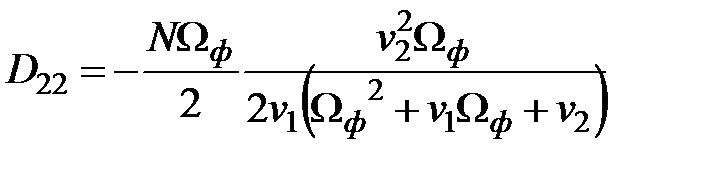 ;
;
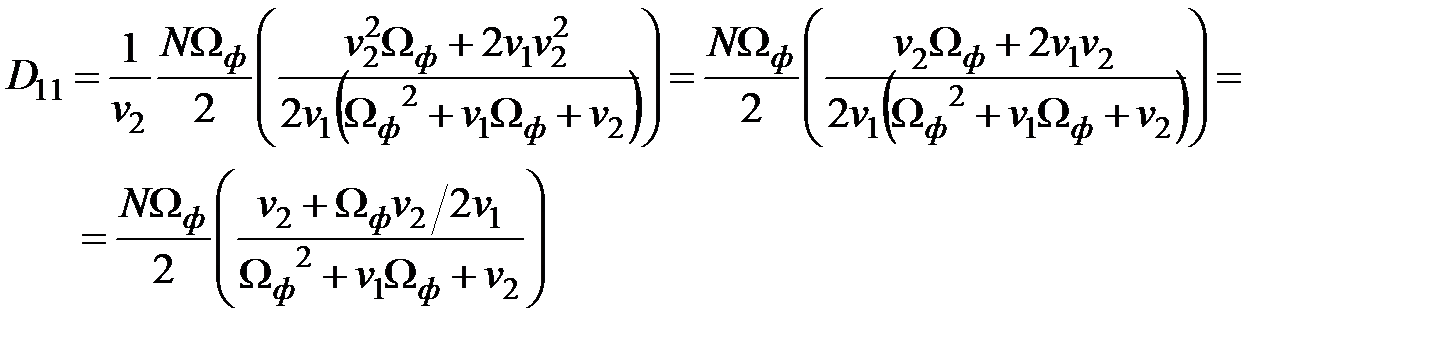
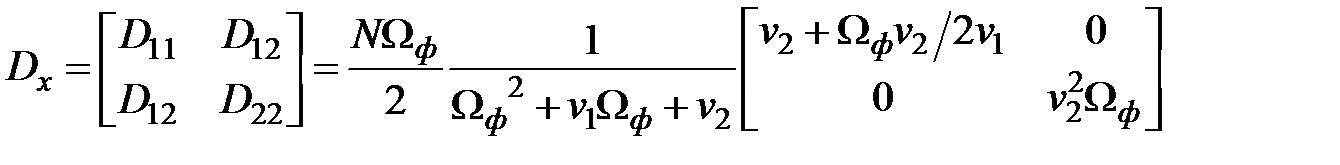
Откуда
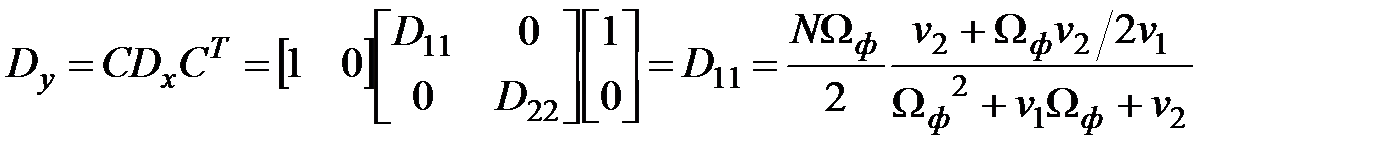
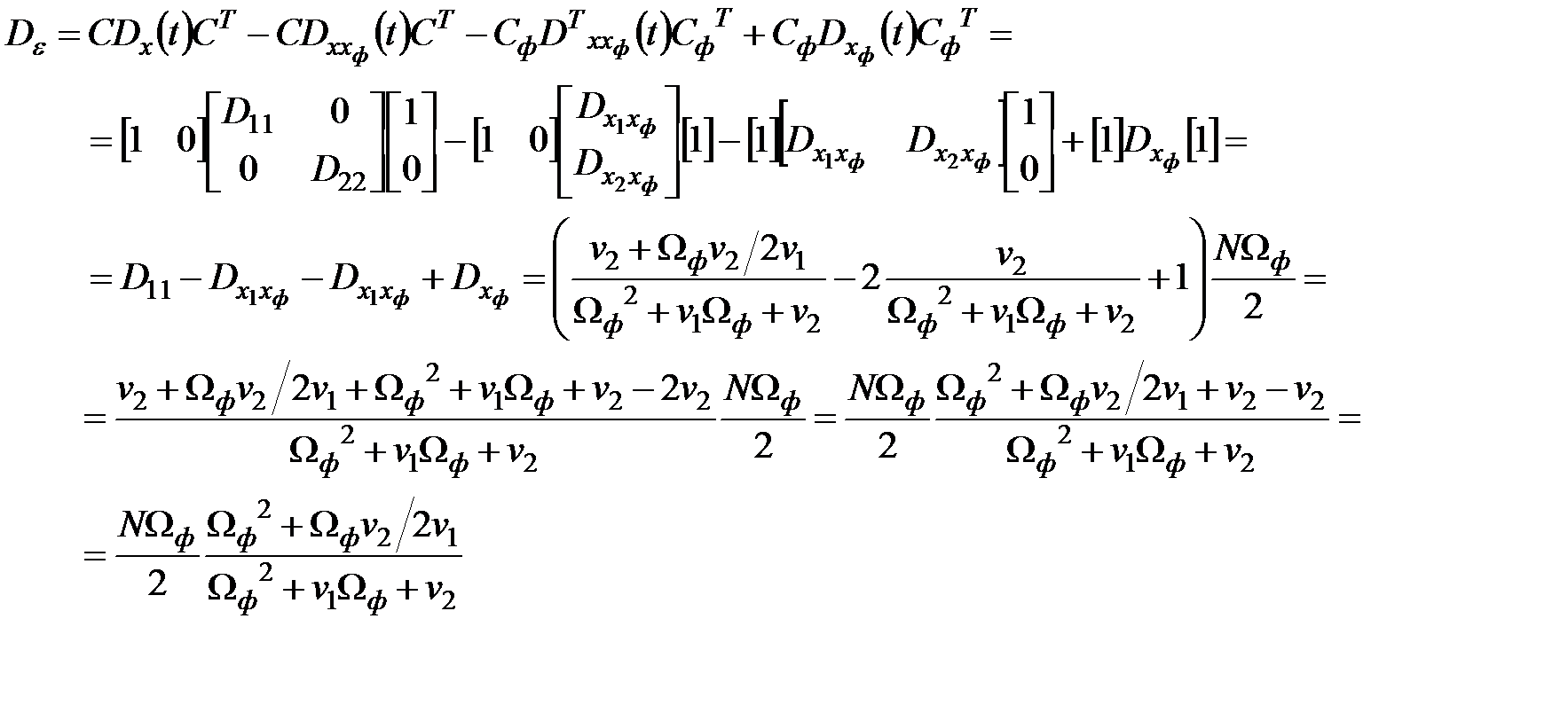
Итак
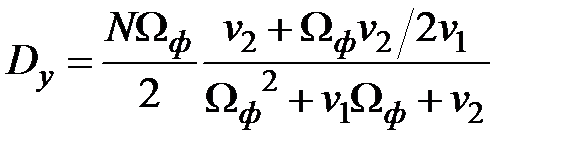
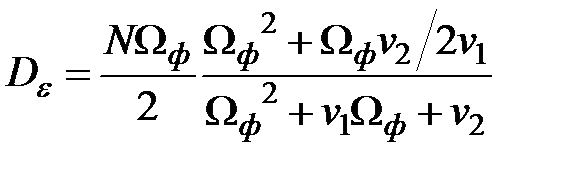
Пример 4.2
Система второго порядка, возбуждаемая окрашенным шумом 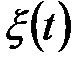 типа «нерегулярная качка»
типа «нерегулярная качка»
Рисунок 4.2 – Структурное представление задачи
(s) 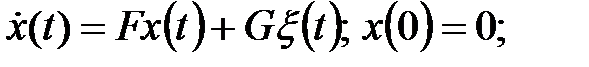
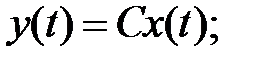
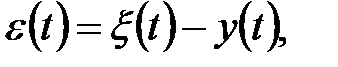
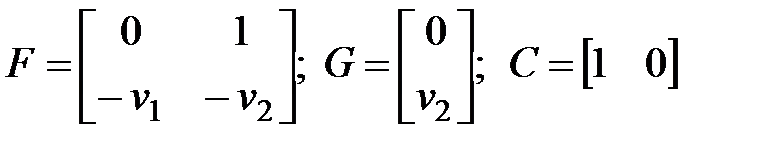
(ФФ) 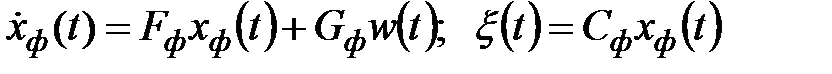 ,
,
где 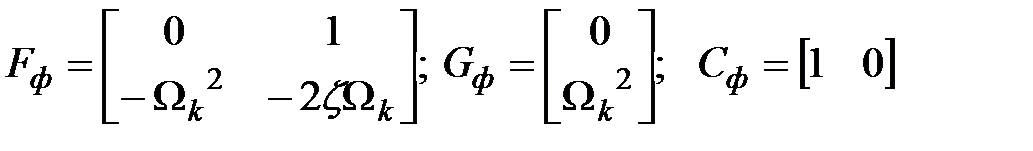 .
.
Найти: 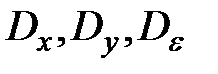 .
.
Решение матричного уравнения 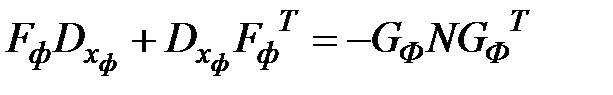
См. пример 3.2.
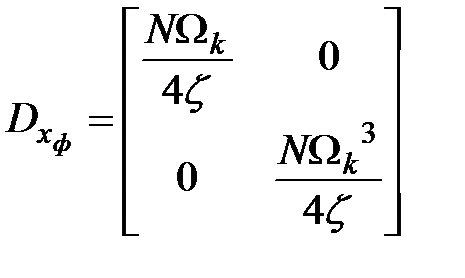 .
.
Решение матричного уравнения 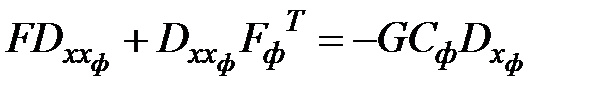
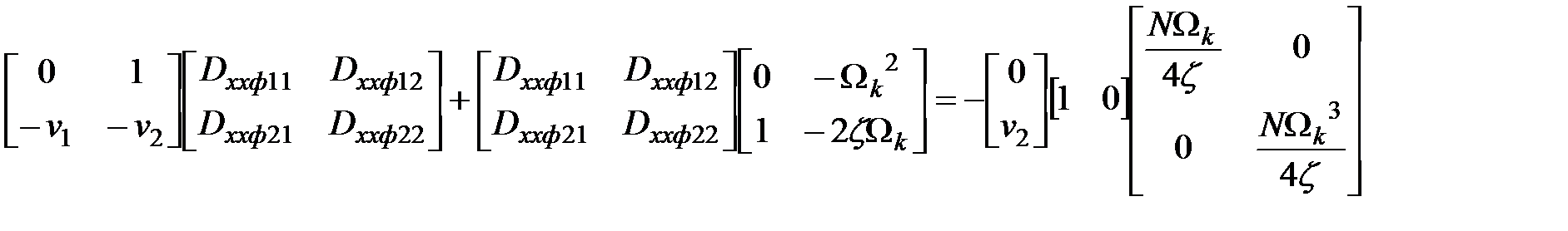
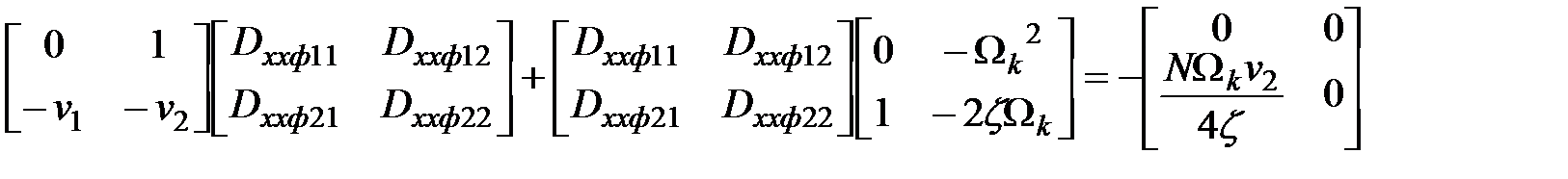
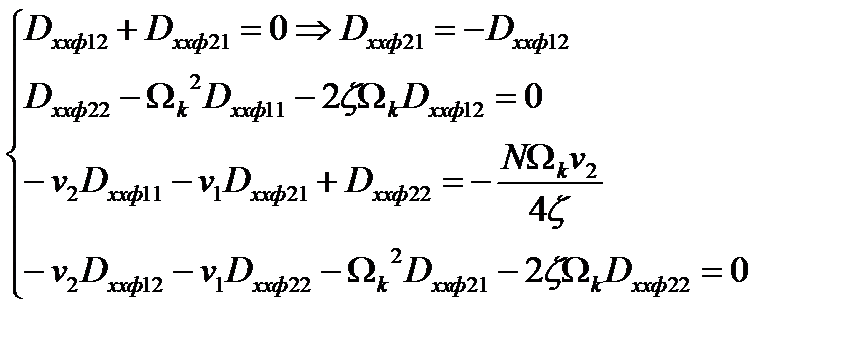
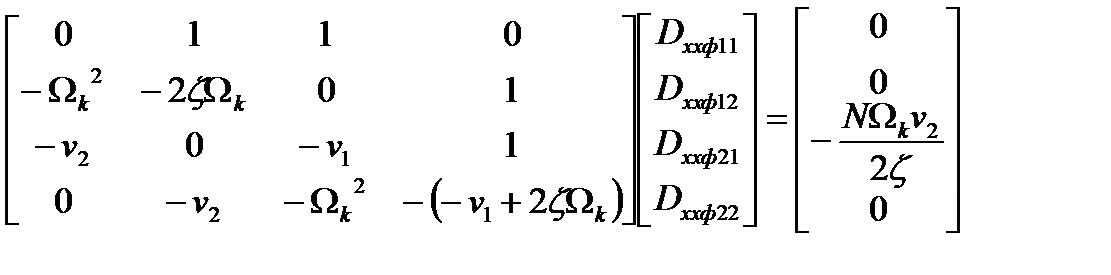
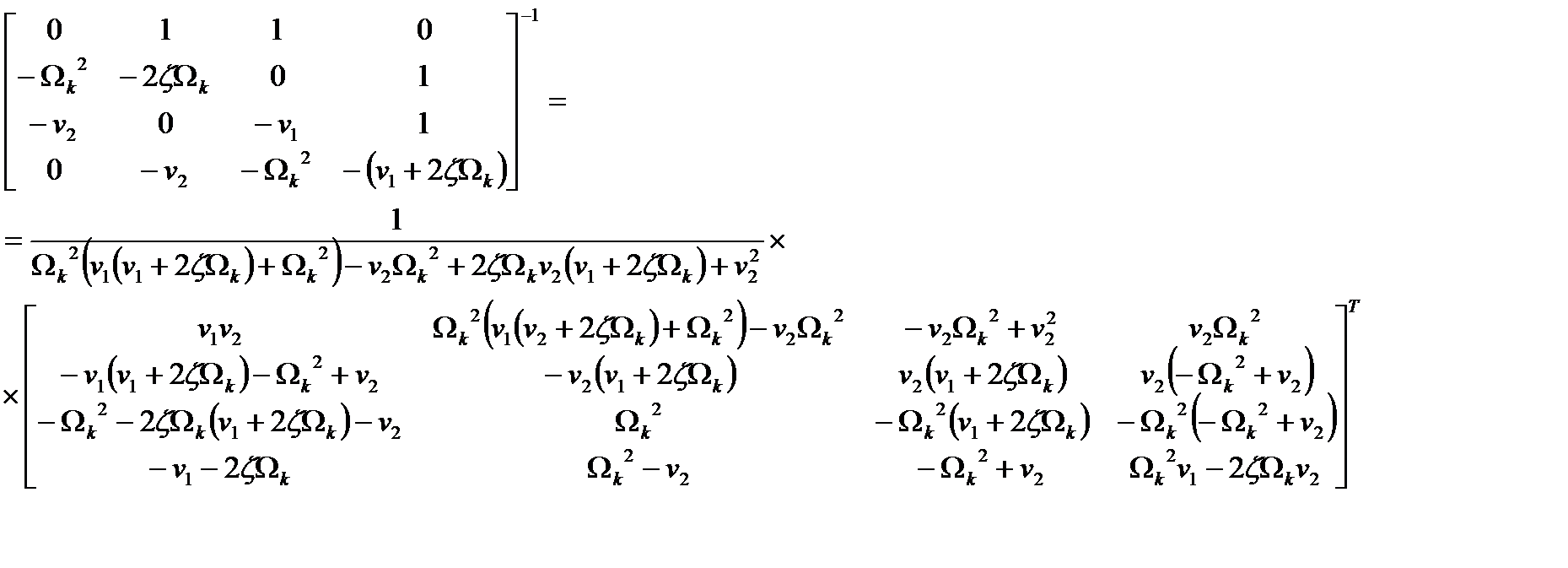
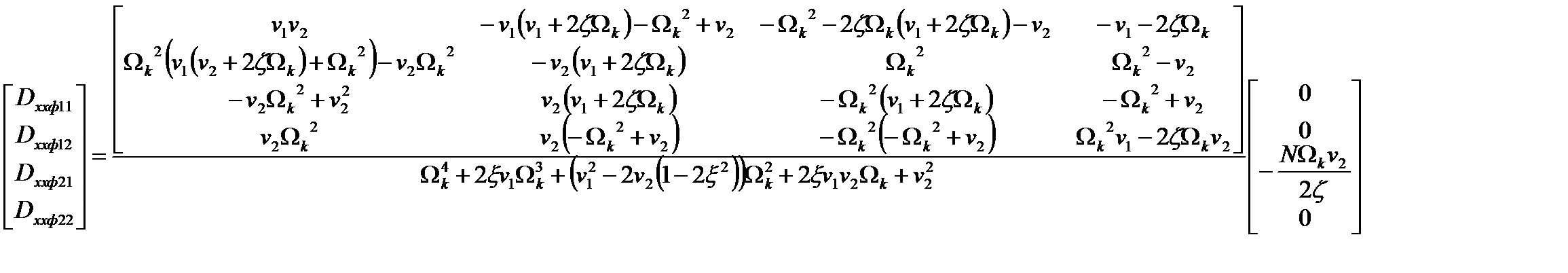
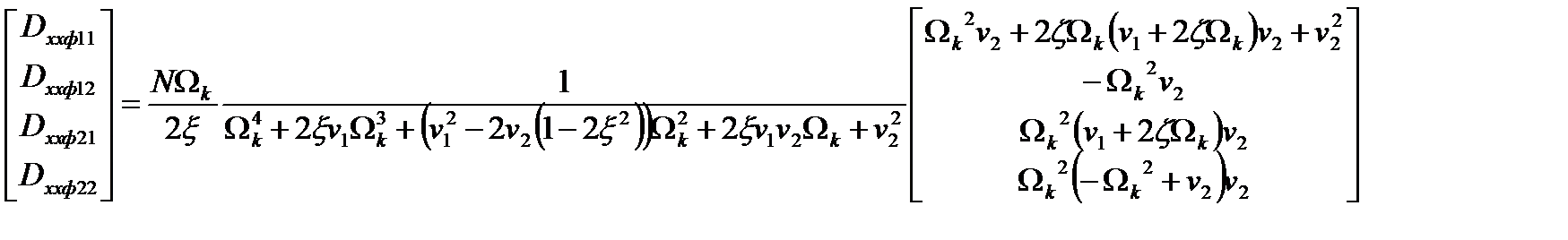
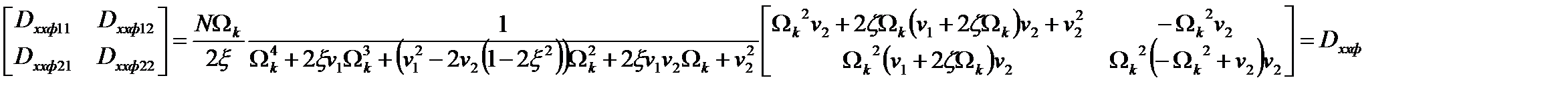
Решение матричного уравнения 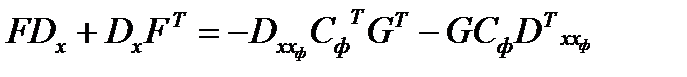
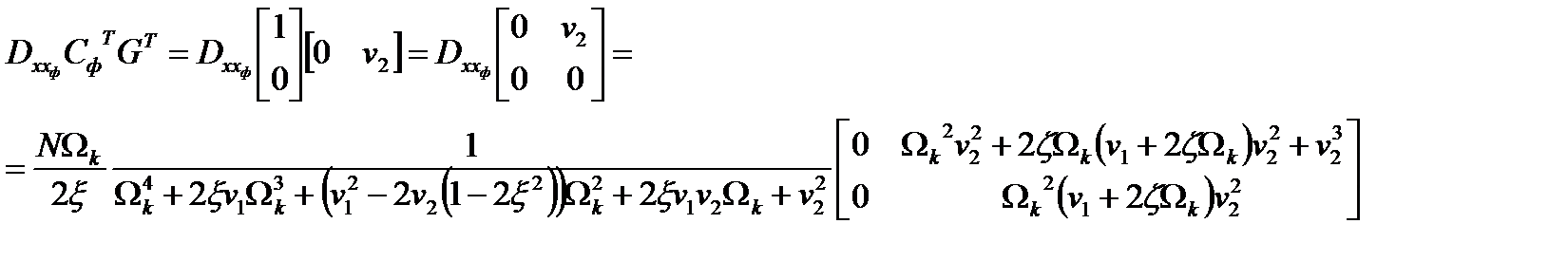
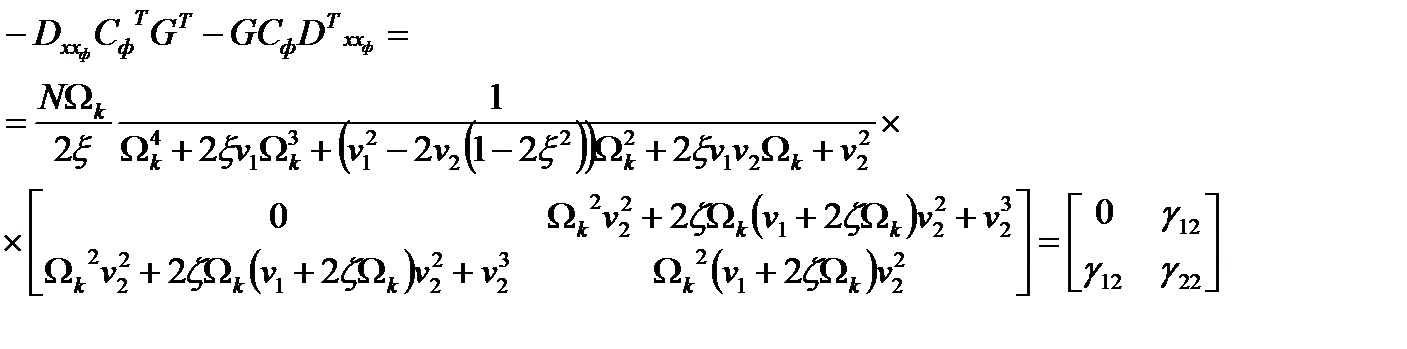
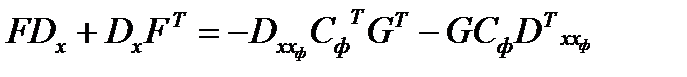
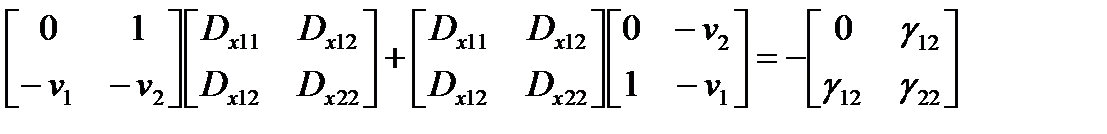
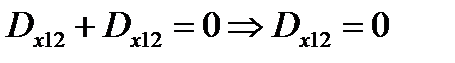
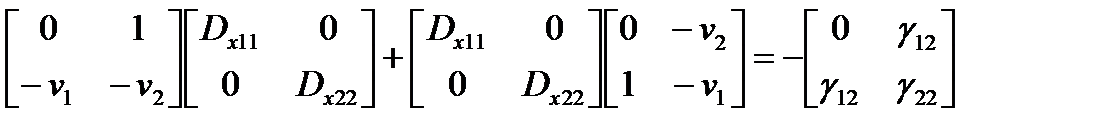
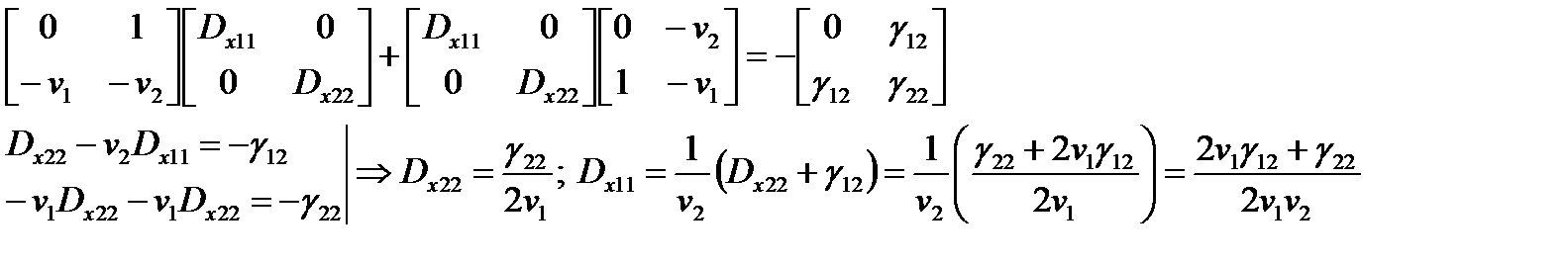
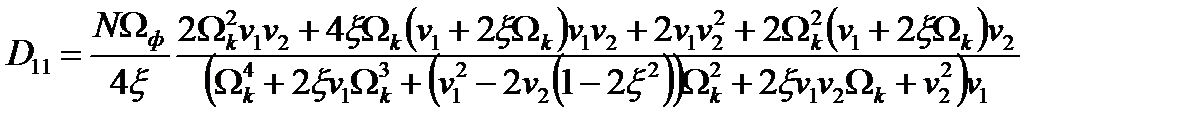 ;
;
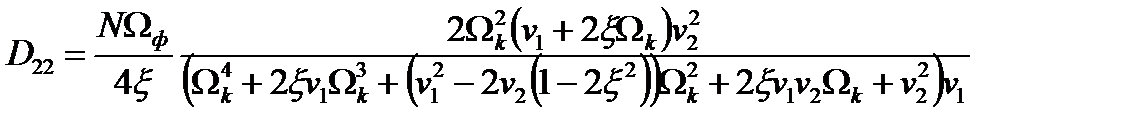 .
.
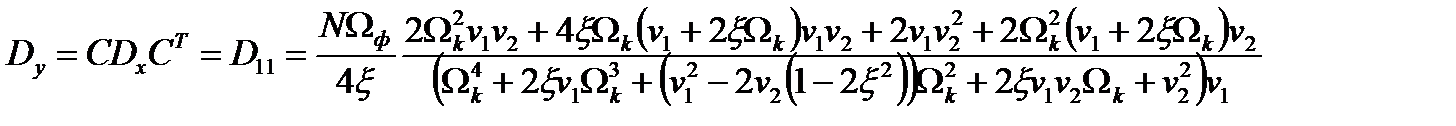 .
.
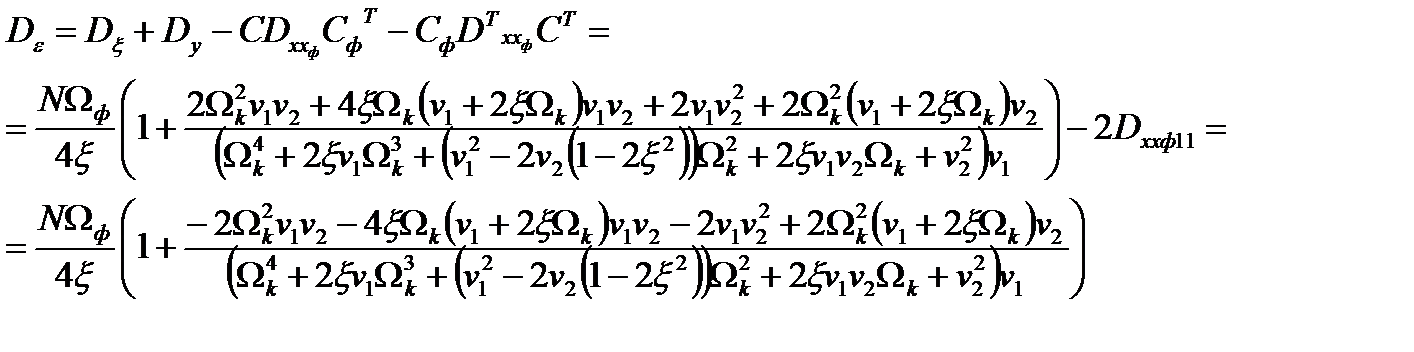
| <== предыдущая страница | | | следующая страница ==> |
| использования аналитических представлений дисперсий выхода и ошибки | | | Тема: Вычисление корреляционной функции и функции спектральной плотности вектора состояния и выхода системы |
Дата добавления: 2014-11-20; просмотров: 339; Нарушение авторских прав

Мы поможем в написании ваших работ!