
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Тема: Вычисление корреляционной функции и функции спектральной плотности вектора состояния и выхода системы
(s) 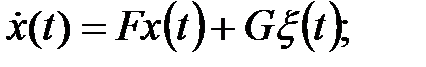
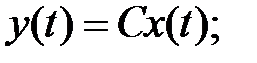
Корреляционная функция 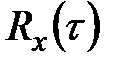 случайной функции
случайной функции 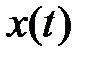 - есть среднее значение произведения двух значений этой функции, сдвинутых на определенный промежуток времени τ, т.е.
- есть среднее значение произведения двух значений этой функции, сдвинутых на определенный промежуток времени τ, т.е.
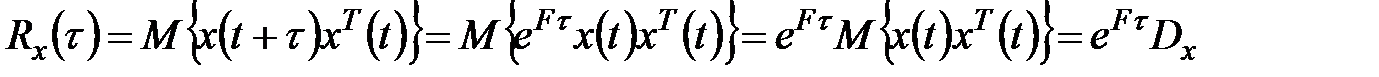 ,
, 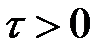 ;
;
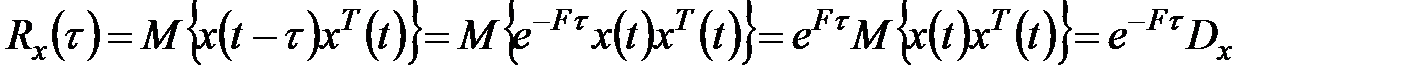 ,
, 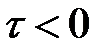 .
.
Корреляционная функция выхода
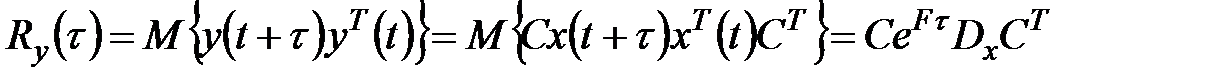 ,
, 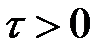 ;
;
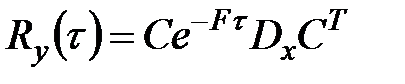 ,
, 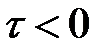 .
.
В случае необходимости воспроизведения корреляционной функции 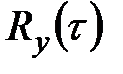 следует воспользоваться автономной версией (s)
следует воспользоваться автономной версией (s) 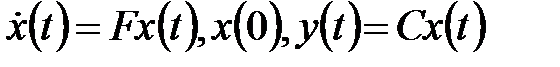 , в которой положить
, в которой положить 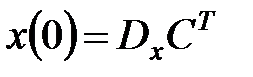 , в результате чего на выходе (s) будет наблюдаться
, в результате чего на выходе (s) будет наблюдаться 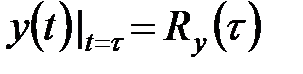 .
.
Интервалом корреляции 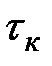 называется величина сдвига по времени, удовлетворяющая условию
называется величина сдвига по времени, удовлетворяющая условию
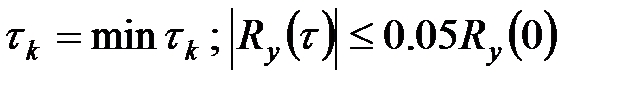 , при
, при 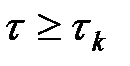 .
.
Рисунок 5.1 – Корреляционная функция выхода
При выборе  отсчеты
отсчеты 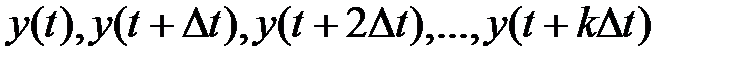 будут некоррелированными.
будут некоррелированными.
Матрица 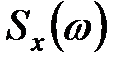 спектральной плотности вектора состояния
спектральной плотности вектора состояния 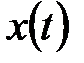 системы (s) как прямое преобразование Фурье
системы (s) как прямое преобразование Фурье 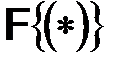 от корреляционной матрицы (функции)
от корреляционной матрицы (функции) 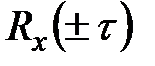
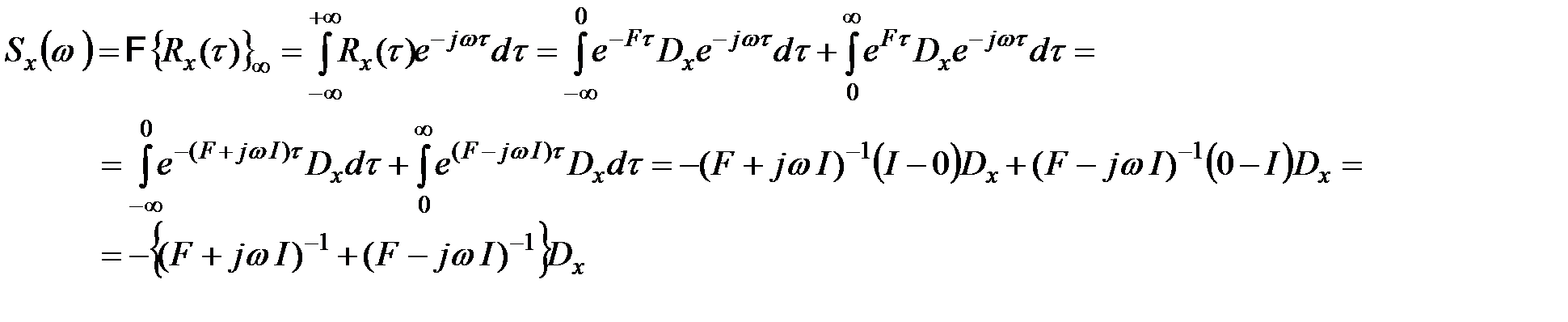
В полученном выражении неявно присутствующую единичную матрицу слева от матрицы 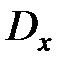 представим в эквивалентной форме
представим в эквивалентной форме
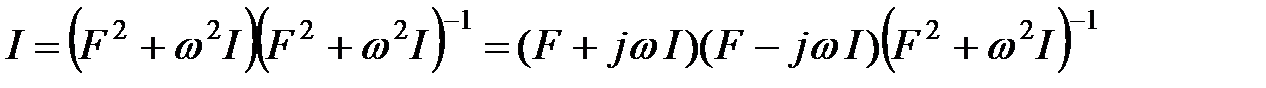 ,
,
что позволяет для матрицы 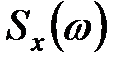 спектральных плотностей вектора состояния
спектральных плотностей вектора состояния 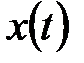 записать
записать
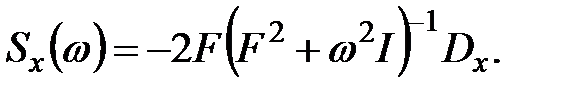
Матрицу 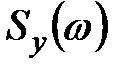 спектральной плотности выхода
спектральной плотности выхода 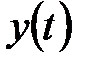 вычислим по формуле
вычислим по формуле
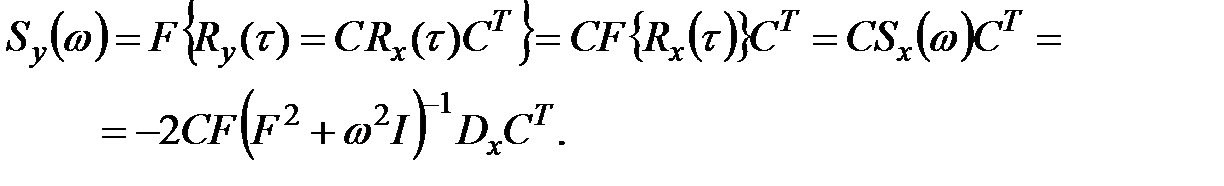
Скалярные оценки процесса 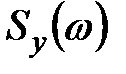 в виде мажоранты и миноранты «эллипсоидного покрытия», конструируемых на максимальном и минимальном элементах спектра сингулярных чисел матрицы.
в виде мажоранты и миноранты «эллипсоидного покрытия», конструируемых на максимальном и минимальном элементах спектра сингулярных чисел матрицы. 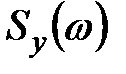
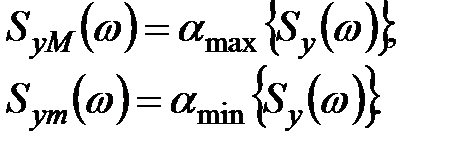
Пример 5.1
ФФ: 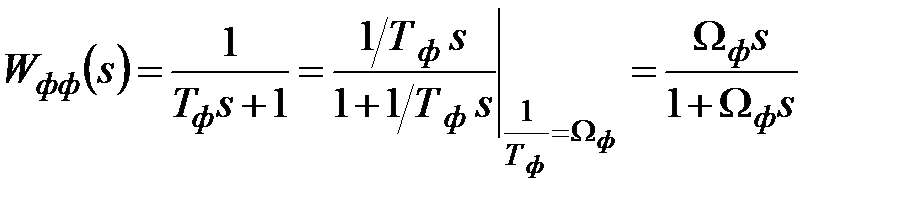
Рисунок 5.2 – Структурное представление ФФ
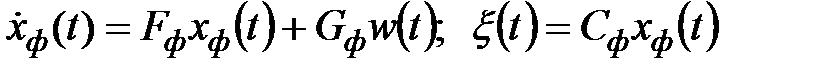 ,
,
где 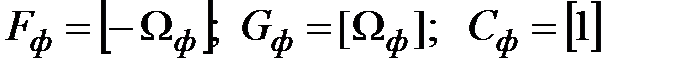 .
.
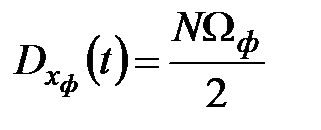
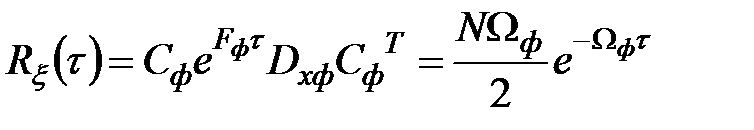 , поэтому
, поэтому 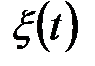 называется экспоненциально коррелированный шум.
называется экспоненциально коррелированный шум.
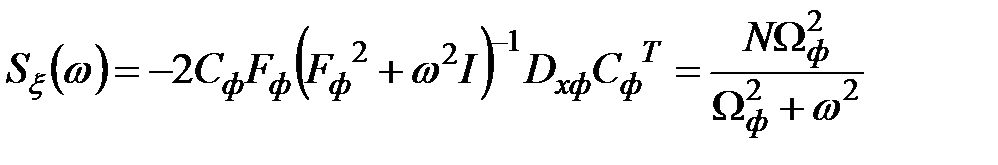 .
.
Пример 5.2
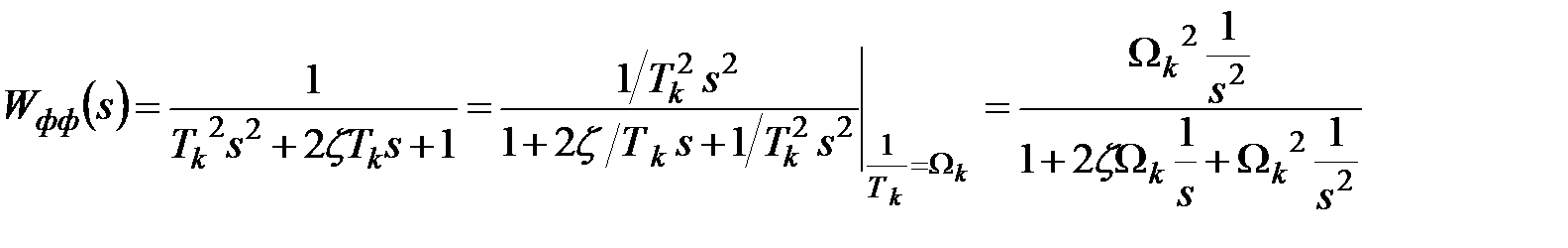
Рисунок 5.3 – Структурное представление ФФ
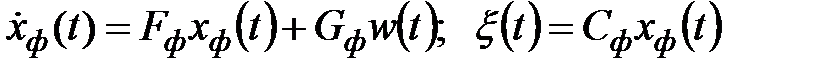 ,
,
где 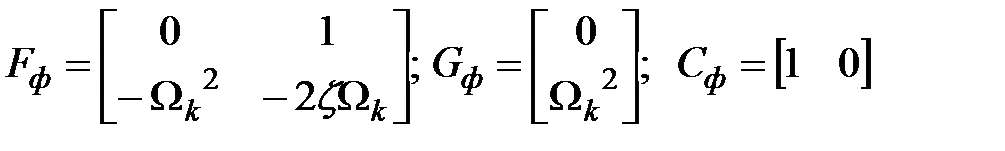 .
.
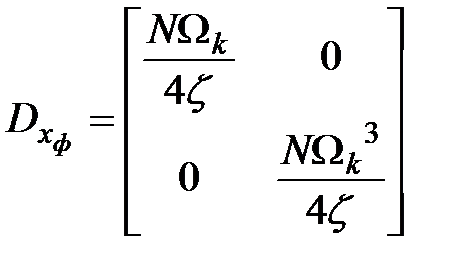
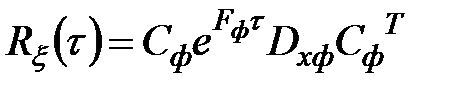
Вычислим матричную экспоненту 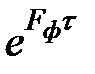 . Представим матрицу
. Представим матрицу 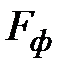 в виде
в виде
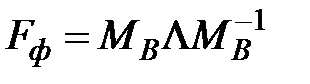 , где
, где 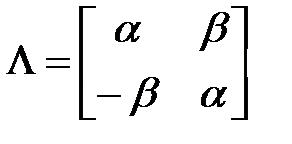 - диагональная матрица, составленная из собственных чисел
- диагональная матрица, составленная из собственных чисел 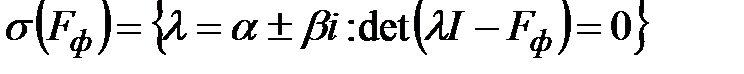 матрицы
матрицы 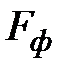 ;
; 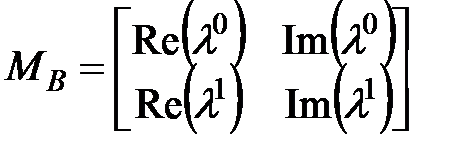 - матрица неособого преобразования подобия, которая при переходе к диагональной форме
- матрица неособого преобразования подобия, которая при переходе к диагональной форме 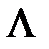 составляется из собственных векторов матрицы
составляется из собственных векторов матрицы 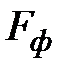 Поскольку
Поскольку 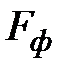 матрица задана в сопровождающей форме, то её собственные вектора составляются по схема Вандермонда.
матрица задана в сопровождающей форме, то её собственные вектора составляются по схема Вандермонда.
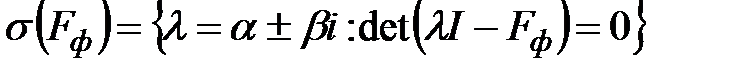
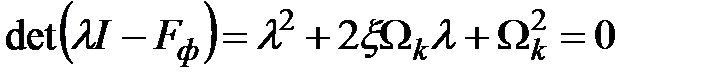
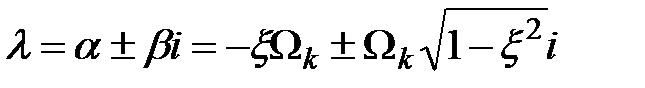 ;
;
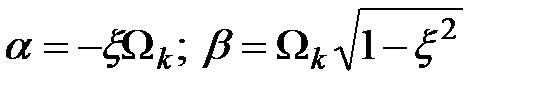
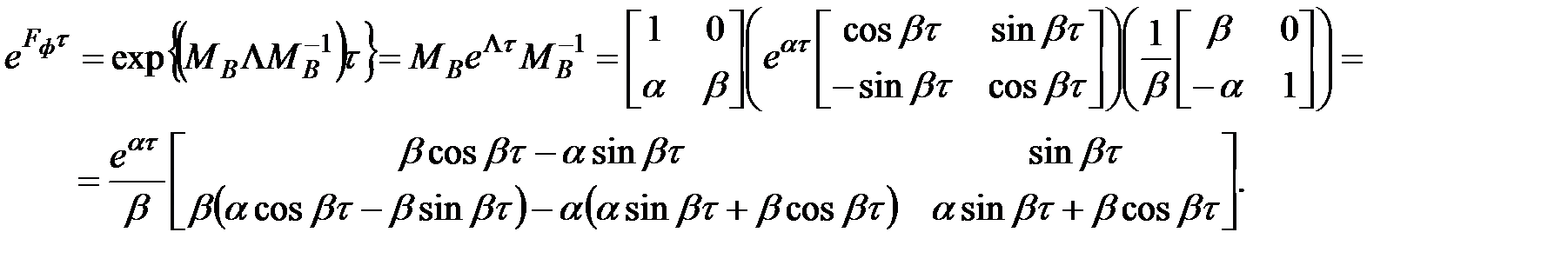
Вернемся к вычислению 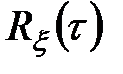

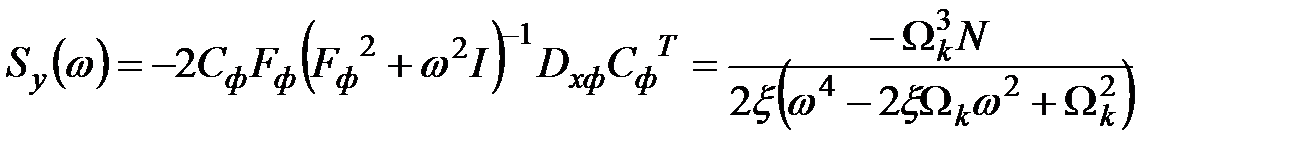
| <== предыдущая страница | | | следующая страница ==> |
| Реакция линейной непрерывной системы на стохастическое воздействие стационарное в широком смысле типа непрерывный «белый шум» | | | Тема 3. ДВИГАТЕЛЬНАЯ АКТИВНОСТЬ - ВАЖНЕЙШЕЕ УСЛОВИЕ ЗДОРОВОГО ОБРАЗА ЖИЗНИ ЧЕЛОВЕКА |
Дата добавления: 2014-11-20; просмотров: 341; Нарушение авторских прав

Мы поможем в написании ваших работ!