Параболоиды

При вращении параболы

x² = 2pz (12.8)

вокруг оси Оz получается поверхность, называемая параболоидом вращения.

Его уравнение получится из уравнения (12.8) путём замены в нём переменной x на выражение :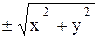

x² + y² = 2pz.

В сечении параболоида вращения плоскостью z = h (ясно, что h ³ 0), перпендикулярной оси Оz, получается окружность (рис. 12.10), уравнения которой будут иметь вид:

(12.9)

Радиус окружности равен r = 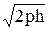, а центр ее лежит на оси Oz. При изменении h от 0 до + ¥ окружность (12.9) будет описывать поверхность, называемую параболоидом вращения.

Возьмём вместо окружности (12.9) эллипс:

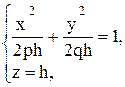(12.10)

где p, q, h – некоторые положительные числа. Полуосями полученного эллипса будут отрезки a = 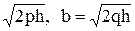. При изменении h от 0 до + ¥ эллипс описывает поверхность, называемую эллиптическим параболоидом.

Его уравнение получается из уравнений (12.10) путём исключения h:

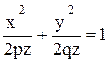, или 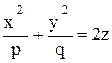. (12.11)

Пересекая эту поверхность плоскостью z = 0, получим в сечении точку (начало координат). Пересекая эту поверхность плоскостями y = 0, x = 0, получим в сечении соответственно две параболы:

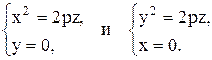
Параболоид имеет две плоскости симметрии: x = 0 и y = 0, которые, пересекаясь, дают его ось симметрии (ось Оz).

Исследуем поверхность параболоида методом сечений.

1) Как уже было отмечено, при пересечении параболоида координатными плоскостями х = 0 и у = 0 получаются две параболы, при z = 0 имеем точку О.

2) Сечение плоскостью z = h (h > 0) определяется уравнениями:

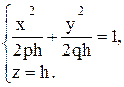
Это - эллипс с полуосями a = 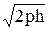и b = 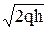. В случае p = q получим параболоид вращения:

2pz = x² + y².

Поскольку x и y входят в уравнение (12.11) в четных степенях, эллиптический параболоид имеет две плоскости симметрии: Оxz и Оyz.

Вопросы на понимание основных понятий:

1. Какое уравнение называется каноническим уравнением конуса?

2. Какое уравнение называется каноническим уравнением эллипсоида?

3. Какое уравнение называется каноническим уравнением однополостного гиперболоида?

4. Какое уравнение называется каноническим уравнением двуполостного гиперболоида?

6. Какое уравнение называется каноническим уравнением параболоида вращения?

4. Технические приложения свойств поверхностей второго порядка

Выдающийся русский инженер Владимир Григорьевич Шухов предложил использовать гиперболоид вращения в строительной технике при сооружении высоких радио- и телевизионных мачт, водонапорных башен. Такие конструкции оказались и весьма прочными. Можно доказать, что фигуру, близкую по форме к форме гиперболоида вращения, можно "построить" следующим способом.

Два круга соединяем между собой отрезками прямых (рис. 12.11, а). Затем верхний круг "проворачиваем" относительно нижнего, не изгибая отрезков прямых (рис. 12.11, б), например против часовой стрелки. Если "совместить" полученную фигуру с такой же, но полученной "поворотом" в противоположную сторону (рис. 12.11, в), в результате и будем иметь нужный гиперболоид.

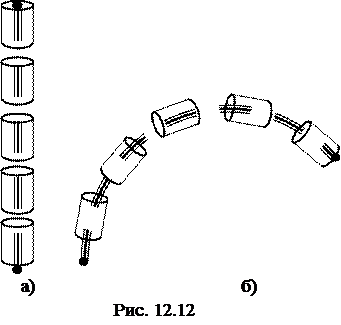Антенны радиостанций малой мощности типа "штырь" обладают свойством изменять свою жесткость: в рабочем положении это довольно жесткий и прочный штырь, в походном его можно легко свернуть в компактное кольцо. Принцип работы такой конструкции заключается в следующем. Если несколько жестких цилиндров "насадить" на общий тросик, а затем с помощью натяжения этого тросика плотно прижать их друг к другу, получится прочная и довольно жесткая конструкция (рис. 12.12, а). При ослаблении натяжения внутреннего тросика (рис. 12.12, б) конструкция теряет былую жесткость, и антенну легко свернуть в небольшое кольцо.

Из всех фигур одинакового объема сфера имеет наименьшую поверхность. Именно поэтому емкости, изготовленные из дорогостоящих материалов, в целях экономии имеют сферическую (или близкую к ней) форму.

Параболоид обладает важным оптическим свойством: если в фокусе поместить источник света, то лучи, падающие на поверхность параболического зеркала, отражаясь, будут идти параллельно оси симметрии параболоида. Поэтому отражающие поверхности прожекторов, автомобильных фар, фонарей и т.д., имеют форму, близкую к поверхности параболоида вращения. На этом же свойстве основано устройство антенн радиорелейной, тропосферной и космической связи, антенн спутникового телевидения, радиолокационных станций и других радиотехнических устройств.

В режиме "передача" радиоволны, попадая из помещенного в фокусе излучателя на поверхность металлического "зеркала тарелки" и отражаясь от нее, распространяются далее узким пучком вдоль оси параболоида, что позволяет при сравнительно небольшой затрачиваемой мощности осуществлять передачу на значительные расстояния.

В режиме "прием" радиоволны сигнала от далекой станции (например со спутника связи) идут почти параллельным пучком. Поэтому, если направить ось параболоида на спутник ("поймать спутник"), то "слабые" сигналы, отражаясь от поверхности "зеркала тарелки", попадут в помещенный в фокусе параболоида приемник уже в виде намного более мощного потока.

Таким образом, на данной лекции мы рассмотрели поверхности второго порядка, их уравнения, а также познакомились с методикой исследования их формы методом сечений.

Повторить основные понятия:

1. Цилиндрические поверхности;

2. Конические поверхности;

3. Поверхности второго порядка: сфера, эллипсоиды, гиперболоиды, параболоиды;

Дата добавления: 2014-11-24; просмотров: 787; Нарушение авторских прав

Мы поможем в написании ваших работ!