Гиперболоиды

Существуют два вида эллиптических гиперболоидов: однополостный и двуполостный.

Определение 12.4. Однополостным гиперболоидом называется поверхность, которая определяется уравнением:

.

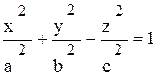1. Рассмотрим сечение его координатной плоскостью Оxz (у = 0). Это сечение определяется уравнениями:

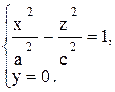
Эта кривая представляет собой гиперболу, расположенную симметрично относительно осей Oх и z. Знак " – " указывает, что действительные полуоси гиперболы расположены на оси Ох, их величина равна а (рис. 12.8), мнимой осью служит ось Oz.

2. Сечение плоскостью Оyz (х = 0) определяется уравнениями:

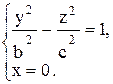
Это - гипербола с действительной осью Oу, соответствующая действительная полуось равна b, мнимой осью служит ось Oz.

3. Теперь рассмотрим сечения гиперболоида плоскостями, параллельными плоскости Oху, т.е. плоскостями вида z = h.

Сечение определяется уравнениями:

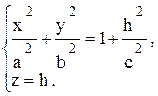
Отсюда видно, что:

1) любая плоскость z = h пересекает гиперболоид по эллипсу с полуосями:

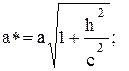
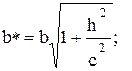
2) величины a*, b* имеют наименьшие значения при h = 0, т.е. на координатной плоскости Оху:

a* = a, b* = b;

если 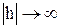, то , .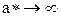

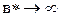На рис.12.8 представлен вид однополостного гиперболоида. Если a = b, то получится однополостный гиперболоид вращения.

Определение 12.5. Двуполостным гиперболоидом называется поверхность, определяемая уравнением

.

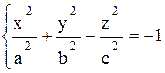1. Сечение плоскостью oxz (у = 0) определяется уравнениями:

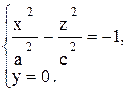
Это - гипербола с действительной осью Oz, соответствующая действительная полуось равна с, мнимой осью служит ось Oх (рис. 12.9).

2. Сечение плоскостью Oyz

(х = 0) определяется уравнениями:

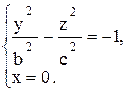
Это - гипербола с действительной осью Oz, соответствующая действительная полуось равна с, мнимой осью служит ось Oу.

3. Рассмотрим сечение плоскостью z = h.

Сечение определяется уравнениями:

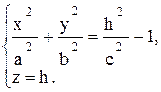(12.7)

Отсюда видно, что:

1) если êh ê> c, то плоскость z = h пересекается гиперболоидом по эллипсу с полуосями:

а*= а 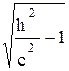, в*= в ;

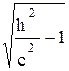2) при возрастании êh ê величины а*, в* возрастают;

3) если êh ê® ¥ , то а*, в* ® ¥;

4) если êh ê® с, то а*® 0, в*® 0;

5) при êh ê< С уравнения (12.7) не имеют действительных решений, определяют так называемый "мнимый эллипс", т.е. плоскость z = h не пересекает поверхность гиперболоида.

Если a = b, то получится двуполостный гиперболоид вращения, при пересечении его плоскостями z = h получаются окружности с центром на оси Oz.

Дата добавления: 2014-11-24; просмотров: 418; Нарушение авторских прав

Мы поможем в написании ваших работ!