Эллипсоиды

Определение 12.3. Эллипсоидом называется поверхность, которая в декартовой системе координат определяется уравнением

.

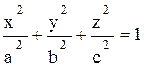Это каноническое уравнение эллипсоида.

Для установления формы эллипсоида применим так называемый метод "параллельных сечений". Рассмотрим сечения эллипсоида плоскостями, параллельными плоскости Оxy. Уравнение плоскости z = h, а линия, полученная в сечении, определяется уравнениями:

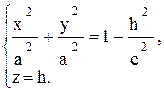
Отсюда видно, что:

1) при | h | < c плоскость z = h пересекает нашу фигуру по эллипсу с полуосями:

, ;

2) при h = 0, a* = a, b* = b – имеют наибольшее значение;

3) при возрастании 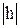a* и b* убывают;

4) при h = ± c a* = 0, b* = 0, т.е. эллипс вырождается в точку;

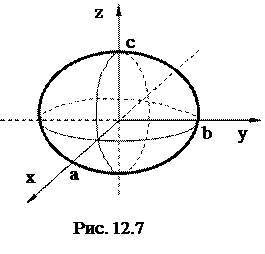5) при 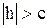- уравнения определяют мнимый эллипс, т.е. секущая плоскость z = h не пересекает поверхность.

Аналогично можно рассмотреть сечения эллипсоида плоскостями, параллельными плоскостям Оxz и Оyz. Заключаем, что эллипсоид есть замкнутая овальная поверхность, имеющая три перпендикулярные плоскости симметрии (рис. 12.7).

Величины a, b, c называются полуосями эллипсоида. Если они различны, эллипсоид называется трёхосным.

Если a = b = c, то эллипсоид является сферой. Если равными являются две полуоси, то получим эллипсоид вращения.

Дата добавления: 2014-11-24; просмотров: 434; Нарушение авторских прав

Мы поможем в написании ваших работ!