Поверхности второго порядка

Сфера

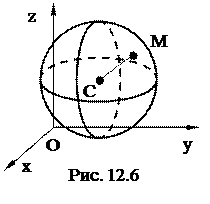
Определение 12.2. Сферической поверхностью или просто сферой называется геометрическое место точек пространства, равноудалённых от одной точки, называемой центром сферы (рис.12.6).

Пусть известны координаты центра сферы С(a, b, c) и радиус R. Пусть M(x, y, z) – любая точка на сфере, тогда, по определению сферы, :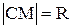

.

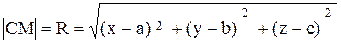Возведя обе части в квадрат, получим уравнение сферы

(x - a)² + (y - b)² + (z - c)² = R² .

Если a = b = c = 0, то центр находится в начале координат и уравнение сферы примет вид

x² + y² + z² = R².

Раскроем скобки в общем уравнении сферы:

x² + y² + b² – 2ax – 2by - 2cz +a² + b² + c² – R² = 0.

Получили уравнение второй степени. Но не всякое уравнение второй степени определяет сферу. Основные признаки сферы:

1) коэффициенты при x, y, z равны;

2) коэффициенты при xy, yz, zx равны нулю.

Дата добавления: 2014-11-24; просмотров: 323; Нарушение авторских прав

Мы поможем в написании ваших работ!