Конус вращения

Рассмотрим прямую

z = 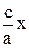, (12.2)

лежащую в плоскости Оxz. При вращении её вокруг оси Оz образуется поверхность, называемая конусом вращения (рис. 12.5).

Уравнение конуса вращения получится из уравнения (12.2), если в нём заменить переменную x выражением 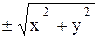: z = .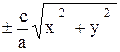

После возведения в квадрат обеих частей последнего уравнения мы получим уравнение конуса вращения в виде

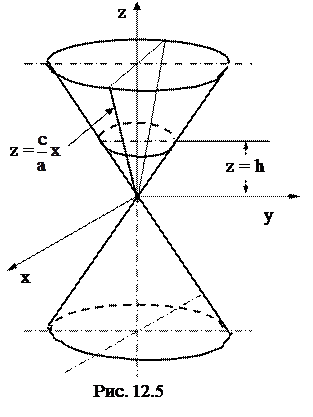
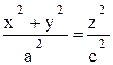. (12.3)

В сечении конуса (12.3) плоскостью z = h получается окружность, уравнение которой имеет вид

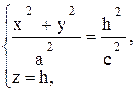(12.4)

которую можно рассматривать как направляющую конуса вращения.

Если вместо окружности (12.4) за направляющую взять эллипс:

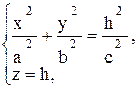(12.5)

то при непрерывном изменении h от - ¥ до + ¥ эллипс (12.5) будет перемещаться в пространстве и, оставаясь параллельным плоскости Оxy, опишет конус с эллиптической направляющей. Уравнение конуса получится путём исключения h из уравнений (12.5):

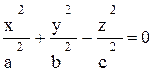. (12.6)

При a = b уравнение (12.6) обращается в уравнение (12.3) и определяет конус вращения.

Дата добавления: 2014-11-24; просмотров: 280; Нарушение авторских прав

Мы поможем в написании ваших работ!