Общие теоремы динамики

Для решения задач во многих случаях оказывается более удобным пользоваться так называемыми общими теоремами динамики, являющимися следствиями основного уравнения динамики. Эти теоремы:

1) Устанавливают наглядные зависимости между основными динамическими характеристиками движения материальных тел.

2) Позволяют изучать отдельные стороны явления, а не в целом.

3) Избавляют, в некоторых случаях, от необходимости интегрировать дифференциальные уравнения движения, упрощая процесс решения.

2.2.1 Теорема о движении центра масс

Формулировка теоремы:

Центр масс механической системы движется так, как двигалась бы точка с массой, равной массе механической системы, при действии на нее всех внешних сил, приложенных к системе.

Аналитические выражения теоремы – это уравнения (1). При решении задач часто в сочетании с уравнениями (1) используются формулы для нахождения координат центра масс системы по координатам ее точек или центров масс отдельных частей системы:

;

; (4)

,

где m_ν – масса ν-й точки или части механической системы.

Путем дифференцирования по времени уравнений (4) получаются связи между проекциями на координатные оси скорости центра масс системы и одноименными проекциями скоростей точек (или скоростей центров масс отдельных частей) системы:

;

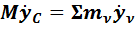; (5)

.

Если продифференцировать по времени последние уравнения еще раз получаются связи между проекциями на координатные оси ускорения центра масс системы и одноименными проекциями ускорений точек (или ускорений центров масс отдельных частей) системы:

;

; (6)

.

Дата добавления: 2014-12-09; просмотров: 176; Нарушение авторских прав

Мы поможем в написании ваших работ!