
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Неопределенный интеграл. Основные методы интегрирования
Справочный материал
1. Первообразной функции f(x) на промежутке Х называется такая функция F(x), что
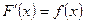 или
или 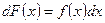 ,
, 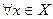 .
.
2. Неопределенный интеграл от функции f(x) – это совокупность всех первообразных данной функции на промежутке X
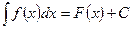 .
.
Операция нахождения неопределенного интеграла называется интегрированием.
Свойства неопределенного интеграла:
1° 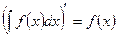 или
или 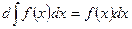
2° 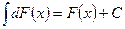
3° 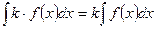
4° 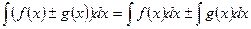
5° Инвариантность формулы интегрирования:
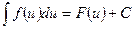 , где
, где 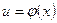 - непрерывно дифференцируемая функция и
- непрерывно дифференцируемая функция и 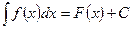
3. Методы интегрирования
Непосредственное интегрирование. В результате тождественных преобразований подынтегральной функции и применения свойств 3°, 4° данный интеграл сводится к табличным интегралам.
Метод замены переменной
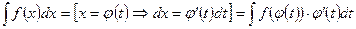
Применение метода замены переменной:
а) Линейная подстановка
Теорема. Если 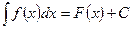 , то
, то 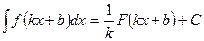
б) Подынтегральное выражение содержит дифференциал некоторой функции, которую можно взять в качестве новой переменной: 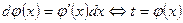
в) Подынтегральная функция является сложной. Промежуточный аргумент можно взять в качестве новой переменной.
Метод интегрирования по частям : 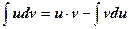
(1) 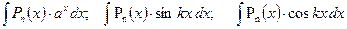 ;
;
(2) 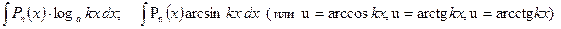
(3) 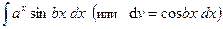
Интегрирование функций, содержащих квадратный трехчлен
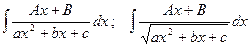
1.Выделение полного квадрата: 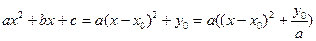
2.Введение новой переменной: 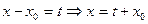 ,
, 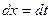
3.Вычисление полученных табличных интегралов.
Задачи
1. Вычислить интегралы, используя метод непосредственного интегрирования
1. 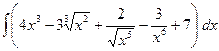 4.
4. 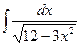 5.
5. 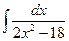
2. 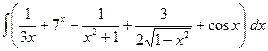 6.
6. 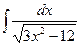 7.
7. 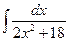 .
.
3. 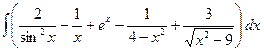
| <== предыдущая страница | | | следующая страница ==> |
| регулирования | | | Вычислить интегралы, используя линейную подстановку |
Дата добавления: 2014-12-09; просмотров: 203; Нарушение авторских прав

Мы поможем в написании ваших работ!