Понятие нечеткого множества и операций над ним

Применение нечеткой логики в ИИС

Математическая теория нечетких множеств, созданная для распознавания образов, в настоящее время имеет приложения в самых различных областях научной и хозяйственной деятельности. В частности, нечеткие множества нашли свое применение в работах по искусственному интеллекту и при управлении сложными экономическими процессами и системами.

В основе данной теории лежат понятия нечеткого множества и функции принадлежности. Пусть E — множество, счетное или нет, и х — элемент E. Тогда нечеткое подмножество А множества E определяется как множество упорядоченных пар , , где — характеристическая функция принадлежности, принимающая свои значения во вполне упорядоченном множестве M, указывающая степень принадлежности элемента x подмножеству А. Множество M называется множеством принадлежностей. Как правило, .

Нечеткое множество называется нормальным если его функция принадлежности достигает значение 1 по крайней мере в одной точке области. Оно называется регулярным, если и только если функция принадлежности имеет только один пик.

Над нечеткими множествами определены все стандартные множественные операции: объединение, пересечение, дополнение, импликация, включение, равенство.

Пусть имеется множество A с функцией принадлежности и множество B с функцией принадлежности . Тогда:

1. Множество С является объединением множеств А и B ( ), если функция принадлежности .

2. Множество С является пересечением множеств А и B ( ), если функция принадлежности .

3. Множество С является дополнением множества А ( ), если функция принадлежности .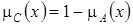

4. Множество С является импликацией множеств А и B ( ), если функция принадлежности .

5. Множество А является включением в множество B ( ), если выполнено .

6. Множество А является равным множеству B ( ) тогда и только тогда, когда .

Дата добавления: 2014-12-09; просмотров: 159; Нарушение авторских прав

Мы поможем в написании ваших работ!