Конспект лекций по математическим моделям в транспортных системах

(специальности ЗА, ЗАБ)

Введение

В современных условиях развития рыночных отношений, договорных цен и стремительного изменения экономической ситуации, выработка эффективных экономических и управленческих решений должна осуществляться на основе анализа всей имеющейся информации о рассматриваемом процессе. Для решения этой задачи в настоящее время широко используются методы математического моделирования.

Моделированиепредставляет собой процесс замещения изучаемого объекта или процесса некоторой его моделью и проведение исследований на модели с целью получения необходимой информации об объекте. В общем случае, под моделью понимается физический или абстрактный образец моделируемого объекта (или процесса), удобный для проведения исследований и позволяющий адекватно отображать интересующие исследователя свойства и характеристики объекта (процесса).

Модели позволяют:

– исследовать свойства реальных объектов и процессов;

– прогнозировать поведение объекта или процесса при различных условиях;

– определять оптимальные способы управления объектами или процессами.

В современных условиях наибольшее распространение получило математическое моделирование, основанное на использовании математических моделей изучаемых объектов и процессов. Масштабное и успешное применение математического моделирования вызвано, в частности, широкими возможностями для его реализации вычислительной техники.

Математическая модель представляет собой приближенное представление реальных объектов, процессов или систем, выраженное в математических терминах и отражающее существенные черты оригинала.

Необходимо отметить тот факт, что в силу высокой сложности изучаемых процессов, учет всех условий реальных задач для построения их математических моделей в большинстве случаев становится невозможным. Поэтому важно понимать, что любая модель представляет оригинал только в некотором определенном смысле. Следовательно, для одного и того же объекта могут быть построены несколько различных математических моделей, отражающих его разные свойства, или описывающих этот объект с разной степенью детализации.

Математическое программирование, представляет собой класс методов, предназначенных для отыскания экстремума заданной функции при определенных ограничениях.

В общем виде задача математического программирования может быть записана следующим образом: определить такие значения переменных , которые доставляют экстремальное значение (т. е. максимум или минимум) функции

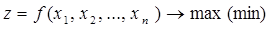(I)

при ограничениях

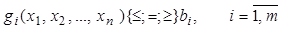. (II)

Величины , так называемые переменные задачи, представляют собой возможные варианты решения, из которых требуется выбрать наилучший вариант.

Функция (I) называется целевой функцией, поскольку она отражает цель оптимизации, т. е. определяет, в каком смысле лучшее решение нас интересует.

Соотношения (II) определяют условия (ограничения) задачи, в которых необходимо принимать решение.

Например, если рассмотреть задачу определения оптимального плана производства продукции различных видов 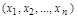, то соотношения (II) описывают имеющиеся ограничения на план выпуска продукции, связанные, например, с существующими запасами сырья, ресурсами, технологическими возможностями производства, лимитами энергетических и трудовых ресурсов и т. д.

Возможные решения называют планамизадачи.

Набор переменных , удовлетворяющий всем соотношениям системы (II) (т.е. всем ограничениям задачи), называется допустимым решением задачи или допустимым планом.

Допустимое решение называется оптимальным решением задачи (I)–(II), или оптимальным планом, если оно доставляет экстремум целевой функции задачи.

В зависимости от типа функций и , различают следующие важнейшие классы задач математического программирования.

Задача (I)–(II) называется задачей линейного программирования, если все функции и , являются линейными функциями относительно переменных . Методы решения задач линейного программирования применяются на промышленных предприятиях при оптимизации производственной программы, распределении ее по цехам, участкам и по временным интервалам, при ассортиментной загрузке оборудования, в задачах текущего, перспективного и технологического планирования, при планировании грузопотоков, определении плана товарооборота и его распределении, составлении оптимальных смесей, решении транспортных и производственно-транспортных задач и т. д.

Если хотя бы одна из функций или , – нелинейна, то задача (I)–(II) называется задачей нелинейного программирования. Нелинейное программирование используется при расчете оптимальной партии выпуска деталей, управлении комплектными поставками и запасами, распределении ограниченных ресурсов, оптимизации некоторых показателей производственно-экономической деятельности и т. д.

Если на переменные наложено условие дискретности (например, целочисленности их значений), то имеем задачу дискретного (целочисленного) программирования. Его методами решаются задачи оптимизации выпуска неделимой продукции, маршрутизации, календарного планирования, управления поставками при заданных транзитных нормах отпуска, размещения производственно-складской структуры и т. п.

– если целевая функция 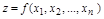имеет специальную структуру, являясь аддитивной или мультипликативной 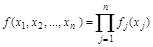, то задача (I)–(II) называется задачей динамического программирования. Таким методом решаются задачи текущего и перспективного планирования, управления производством, запасами и поставками, распределения ограниченных ресурсов, оптимального размещения капитальных вложений, замены оборудования и другие.

1 РЕШЕНИЕ ПРОИЗВОДСТВЕННЫХ ЗАДАЧ МЕТОДАМИ
ЛинейноГО программированиЯ.

1.1 Примеры производственных задач и постановка задачи
линейного программирования

Линейное программирование (ЛП) – раздел математического программирования, содержащий методы отыскания экстремума (максимума или минимума) линейных функций нескольких переменных при линейных ограничениях, наложенных на переменные. В зависимости от типа решаемых задач методы ЛП можно разделить на универсальные и специальные. С помощью универсальных методов могут решаться любые задачи ЛП. Специальные методы учитывают особенности целевой функции и системы ограничений.

Рассмотрим примеры производственных задач, которые могут быть решены методами линейного программирования.

Задача оптимального использования ресурсов. Имеется т видов ресурсов, объемы которых заданы вектором B = ( b₁, b₂,…, b_m ). Задана матрица A=||a_ij||, где a_ij – норма расхода i-го ресурса ( ) на производство единицы j -го вида продукции ( ). Прибыль от выпуска единицы j-го вида продукции составляет р_j. Требуется определить план выпуска продукции X = (x₁, x₂, …, x_n), максимизирующий прибыль предприятия при заданных ресурсах.

Математическая модель задачи может быть записана в следующем виде:

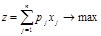(1.1)
при ограничениях:

на затраты ресурсов

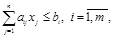(1.2)
условие неотрицательности

(1.3)
В качестве критерия оптимальности в данной задаче также могут быть приняты: минимум затрат на производство продукции, максимум выпуска продукции в стоимостном выражении, максимум использования оборудования и др. Ограничения могут быть связаны с фондом времени работы оборудования, ассортиментом выпускаемой продукции.

Задача распределения парка машин механизированной колонны по участкам земляных работ. Имеется механизированная колонна, располагающая парком из m типов машин. Задана производственная программа колонны на требуемый промежуток времени, в течение которого она должна выполнить земляные работы на n участках. Объем работ на каждом участке равен v_j ( ). Фонд рабочего времени механизмов каждого типа в течение планируемого периода составляет d_i ( ) (машино-смен). Известны также сменная производительность машины i-го типа на j -м участке работ p_ij ( , ) и затраты на разработку 1 м³ грунта на j -м участке с использованием машины i-го типа c_ij ( , ). Требуется найти такой план распределения парка машин механизированной колонны по участкам работ, который обеспечивает выполнение всех работ в полном объеме и с минимальными суммарными приведенными затратами.

Обозначим искомую продолжительность работы в сменах машины i-го типа на j -м участке через x_ij ( , ).

Математическая модель задачи может быть записана в следующем виде:

(1.4)
при ограничениях:

на объем работ на каждом участке, который должен быть выполнен полностью

(1.5)

а фонд рабочего времени машин

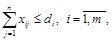(1.6)
условие неотрицательности

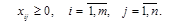(1.7)

Задача размещения звеносборочных баз при ведении укладки пути на рассредоточенных объектах. Строительный трест, ведущий путеукладочные работы на рассредоточенных объектах с небольшими объемами работ, имеет m звеносборочных баз, которые возможно расположить на обслуживаемой территории. Планом предусмотрено n мест укладки пути с объемами работ b_j ( ). Себестоимость сборки и укладки звеньев пути в зависимости от объема сборки на базе составляет c_i ( ) ден. ед., стоимость перевозки 1 км звеньев пути от i-й базы до j -го места укладки пути – t_ij ( , ) ден.ед.

В условиях ведения укладки пути на рассредоточенных объектах возникает необходимость в определении оптимального размещения звеносборочных баз строительных трестов, т. е. такого размещения, при котором суммарные затраты на весь технологический комплекс путеукладочных работ будут минимальными.

Обозначим через x_i ( ) объемы сборки и укладки звеньев пути на i-й базе, а через x_ij ( , ) – объемы звеньев, собранных на i-й базе и укладываемых на j -м объекте.

Математическая модель задачи может быть записана в следующем виде:

(1.8)
при ограничениях:

все собранные на i-й базе звенья пути должны быть уложены на одном или нескольких объектах

(1.9)
объем укладки пути на j -м объекте должен быть обеспечен поставкой звеньев с одной или нескольких баз

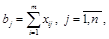(1.10)
общий потребный объем механизированной сборки и укладки пути должен быть равен объему сборки и укладки по всем звеносборочно-укладочным базам

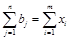, (1.11)
условие неотрицательности

(1.12)

В общем виде задача ЛП сводится к нахождению некоторой совокупности значений переменных X = (x₁, x₂, …, x_n), доставляющих линейной функции цели экстремальное значение и удовлетворяющих системе ограничений в виде равенств или неравенств.

Математическая модель задачи ЛП формулируется следующим образом:

найти план X = (x₁, x₂, …, x_n), который доставляет экстремум функции

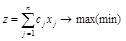(1.13)
при системе ограничений:

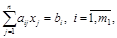(1.14)
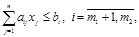(1.15)
(1.16)
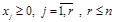. (1.17)
Линейная функция (1.13) называется целевой функцией; множество планов Х, удовлетворяющих системе ограничений (1.14) – (1.17), называется множеством допустимых решений W, 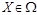. Допустимый план 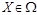, доставляющий целевой функции (1.13) экстремальное значение, называется оптимальным.

Если целевая функция подлежит максимизации, а все ограничения задачи имеют вид равенств и на все переменные величины наложено условие неотрицательности 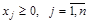, то говорят, что задача представлена в канонической форме записи:

(1.18)
Любую задачу линейного программирования можно свести к задаче линейного программирования в канонической форме записи.

Правило приведения задачи линейного программирования к канонической форме записи состоит в следующем:

1) если в исходной задаче требуется минимизировать целевую функцию z(X), то необходимо перейти от задачи на минимум к задаче на максимум. Очевидно, что максимизация целевой функции z(Х) на области допустимых решений эквивалентна задаче минимизации функции – z (Х) на той же области:

(1.19)

2) если среди ограничений есть неравенства, то необходимо перейти от ограничений в виде неравенств к ограничениям в виде равенств.
Для этого вводят неотрицательные дополнительные переменные x_n+i ³ 0, , которые прибавляются к левым частям ограничений (1.15) и вычитаются из левых частей ограничений (1.16). В целевую функцию (1.13) дополнительные переменные вводятся с коэффициентами, равными нулю;

3) если в исходной задаче на некоторые переменные x_j ( ) не наложено условие неотрицательности, то их представляют в виде разности неотрицательных переменных:

(1.20)

1.2 Геометрическая интерпретация и графическое решение
задачи линейного программирования.

Графический способ решения задач линейного программирования целесообразно использовать для решения задач:

– с двумя переменными, когда ограничения выражены неравенствами;

– со многими переменными при условии, что их можно свести к задачам с двумя переменными.

Пусть задача линейного программирования имеет следующий вид:

(1.21)

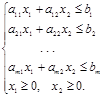(1.22)

Каждое из неравенств (1.22) системы ограничений с геометрической точки зрения определяет на плоскости X₁OX₂ полуплоскость, ограниченную прямой .

Поскольку полуплоскость является выпуклым множеством, а пересечение конечного числа выпуклых множеств также выпукло, то область допустимых решений Ω задачи ЛП является выпуклым множеством. Если же это множество ограничено, то оно называется многоугольником решений.

Приведем несколько примеров областей допустимых решений задачи ЛП (рисунок 1.1).

Рисунок 1.1 – Схемы различных областей допустимых решений:

a – неограниченная область; б – выпуклый многоугольник; в – пустое множество

Целевая функция (1.21) определяет на плоскости семейство параллельных прямых, называемых линиями уровня целевой функции, каждой из которых соответствует определенное значение целевой функции z. Найдем частные производные целевой функции по

Вектор – это вектор наискорейшего возрастания целевой функции, вектор градиентного направления. Направление, противоположное направлению вектора : 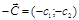, есть направление наискорейшего убывания целевой функцииили антиградиентное.

Графический метод решения задачи линейного программирования состоит в следующем. Выбираем произвольное положение линии уровня целевой функции z,например, z = 0. Перемещаем прямую z = 0 в направлении вектора . При некотором значении z эта прямая впервые коснется области допустимых решений Ω. В данной точке (или точках) целевая функция достигает минимума. При дальнейшем перемещении прямой z по направлению вектора 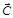она коснется области допустимых решений Ω в последней точке (или точках). В данной точке (точках) целевая функция достигает максимума. Если же область Ω не ограничена, то сколько бы прямую ни перемещали в направлении вектора 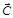, она будет иметь общие точки с областью решений Ω. В этом случае целевая функция не ограничена.

Алгоритм графического решения задачи ЛПв случае двух переменных:

Шаг 1 Построить область допустимых решений Ω с учетом системы ограничений (1.22).

Шаг 2 Построить вектор 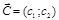наискорейшего возрастания целевой функции – вектор градиентного направления.

Шаг 3 Провести произвольную линию уровня целевой функции z=const, перпендикулярную к вектору .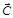

Шаг 4 При решении задачи на максимум перемещать прямую z=const в направлении вектора 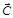, пока она не коснется области допустимых решений Ω в последней точке. В случае решения задачи на минимум линию уровня целевой функции z=const перемещать в антиградиентном направлении до последней точки касания с областью допустимых решений Ω.

Шаг 5 Определить оптимальный план 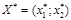. Возможны следующие случаи:

а) оптимальный план единственный. Тогда линия уровня и область допустимых решений Ω в крайнем положении будут иметь одну общую точку (рисунок 1.2: a – на mах и min, б – на min);

б) оптимальных планов может быть бесконечное множество. В этом случае в крайнем положении линия уровня проходит через грань области Ω (рисунок 1.2: б – на mах, в – на min);

в) целевая функция не ограничена. Линия уровня, сколько бы ее ни перемещали, будет иметь общие точки с областью допустимых решений Ω (рисунок 1.2: в – на mах, г – на mах и min);

г) задача решения не имеет. Область допустимых решений – пустое множество, т. е. система ограничений (1.17) несовместна (рисунок 1.2, д).

Шаг 6 Вычислить значение целевой функции по формуле (1.16).

Рисунок 1.2 – Варианты ситуаций при решении задач ЛП графическим методом

Рассмотрим пример решения задачи линейного программирования графическим методом.

Дата добавления: 2014-12-09; просмотров: 399; Нарушение авторских прав

Мы поможем в написании ваших работ!