Относительная флуктуация

Среднее квадратичное величины

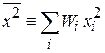. (1.7)

Дисперсия–­ среднее квадратичное отклонение от среднего

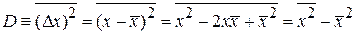. (1.8)

Флуктуация – корень квадратный из дисперсии

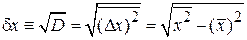. (1.9)

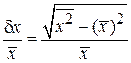. (1.10)

Если x случайным образом изменяется с течением времени, то относительная флуктуация показывает долю времени, в течение которой система находится в состоянии с .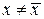

Теорема: Относительная флуктуация аддитивной величины, характеризующей систему, уменьшается обратно пропорционально корню квадратному из числа независимых подсистем и для макроскопической системы она мала. Примером аддитивной величины (от лат. additivus – «прибавляемый») является энергия. Флуктуация энергии для макросистемы ничтожно мала, для микросистемы она существенна.

Доказательство

Аддитивная величина X для системы равна сумме значений x_k для N независимых подсистем или частиц

.

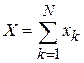По свойству 2 усреднения – среднее от суммы равно сумме средних

.

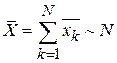Получаем отклонение от среднего

.

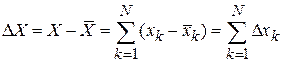Дисперсия равна

.

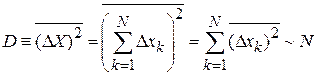При возведении в квадрат 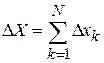и усреднении результата для перекрестных произведений учтено свойство 3 усреднения – среднее от произведения независимых величин равно произведению их средних

, ,

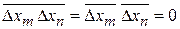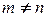и использовано, что среднее отклонение от среднего равно нулю

.

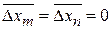Не равными нулю остаются квадраты величин. В результате

.

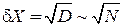Относительная флуктуация

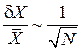(П1.11)

уменьшается обратно пропорционально корню квадратному из числа независимых подсистем.

Производящая функция. Имеется случайная величина n, которая можем принимать дискретные значения в интервале 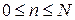. Вероятность получения результата n равна 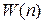. Определяем производящую функцию в виде

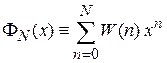. (П1.14)

Если известна производящая функция, то распределение вероятности получаем из (П1.14)

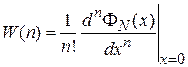, (П1.15)

где использовано

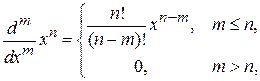
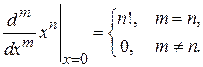
Условие нормировки (1.6)

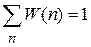
требует

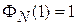. (П1.16)

Для получения средних значений случайной величины дифференцируем (П1.14)

,

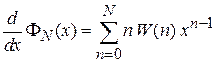и находим

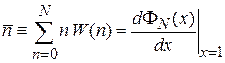. (П1.17)

Двукратное дифференцирование (1.14)

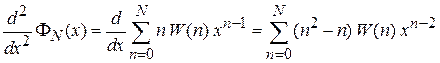
дает

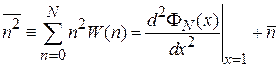. (П1.18)

Использование производящей функции упрощает получение соотношений между вероятностными характеристиками.

ХАРАКТЕРИСТИКИ СЛУЧАЙНой

НЕПРЕРЫВНой ВЕЛИЧИНы

Плотность вероятности. Имеется случайная величина x, которая можем принимать непрерывной значения. Вероятности обнаружения x в единичном интервалеоколо выбранного значения называется плотностью вероятности результата

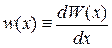. (1.11)

Сравните с определением скорости 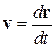, которая является перемещением за единицу времени. Вероятность получения результата в интервале 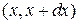равна

.

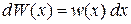Пример: Пусть 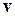– скорость частицы идеального газа. Вероятность обнаружения частицы со скоростью в интервале 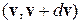равна

,

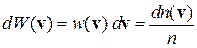где

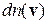– концентрация частиц со скоростями в интервале ;

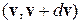n – концентрация частиц со всеми скоростями;

плотность вероятности

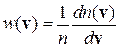
– вероятность обнаружения частицы со скоростью в единичном интервале около значения v.

Условие нормировки для непрерывного распределения

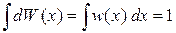. (1.12)

Дата добавления: 2014-02-27; просмотров: 1029; Нарушение авторских прав

Мы поможем в написании ваших работ!