Постановка задачи. Методы решения алгебраических и трансцендентных уравнений

Методы решения алгебраических и трансцендентных уравнений.

Прежде всего, вспомним основные понятия.

Пусть задано уравнение вида

,

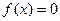(1)

где 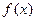- алгебраическая или трансцендентная функция определенная и непрерывная на некотором промежутке.

Функция 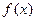называется алгебраической, если над неизвестными производятся только операции сложения, вычитания, умножения, деления, возведения в степень и извлечение корня, в противном случае функция называется трансцендентной.

Корнями уравнения (1) или нулями функции 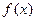называются числа, которые путем подстановки их в (1) превращают это уравнение в верное числовое равенство.

Число 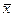есть корень уравнения (1) кратности k ,если при 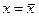вместе с функцией 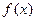обращаются в нуль ее производные до (k-1)-го порядка включительно, т.е. 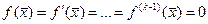, а 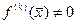. При k=1 корень называется простым.

Решить уравнение (1), значит, решить две задачи:

1) отделить корни, т.е. установить количество корней и указать как можно более «точные» промежутки, в которых находятся по одному простому или кратному корню;

2) уточнить корни, т.е. на найденных промежутках вычислить корни с заданной точностью.

Мы будем рассматривать методы поиска только действительных корней.

Заметим, что все численные методы решения нелинейных уравнений являются приближенными и дают приближенное решение с некоторой заданной точностью. Среди приближенных методов выделить итерационные методы, которые основаны на использовании повторяющегося (циклического процесса) и позволяют получить решение в результате последовательных приближений. Операции, входящие в повторяющийся процесс, составляют итерацию. Итерация – это последовательное приближение к решению.

Дата добавления: 2014-12-09; просмотров: 230; Нарушение авторских прав

Мы поможем в написании ваших работ!