Имитационное моделирование системы массового обслуживания с одним устройством обслуживания

Цель работы: изучить основные принципы имитационного моделирования на примере моделирования простейшей системы массового обслуживания с одним устройством обслуживания..

Краткие теоретические сведения

Дискретно-событийное моделирование используется для построения модели, от­ражающей развитие системы во времени, когда состояния переменных меняются мгновенно в конкретные моменты времени. В такие моменты времени происходят события, при этом событие определяется как мгновенное возникновение, которое может изменить состояние системы.

Теоретически дискретно-событийное моделирование можно осуществлять с помощью вычислений вручную. Однако, на практике количество данных, которые должны сохранять­ся и обрабатываться при моделировании большинства реальных систем, диктует необходимость применения вычислительных машин.

Пример 1. Рассмотрим систему с одним устройством обслуживания, например парик­махерскую или справочное бюро в аэропорту с одним оператором. Нам необходимо приблизительно подсчитать ожидаемую среднюю задержку требований в очереди. При этом задержка требования в очереди равна времени, прошедшему с момента его появле­ния в системе до начала его обслуживания.

Для того чтобы рассчитать среднюю задерж­ку в дискретно-событийной имитационной модели, определяются такие переменные состояния, как состояние устройства обслуживания (занято или свободно), число тре­бований в очереди (если таковые имеются) и время поступления каждого требования, ожидающего своей очереди.

При поступлении требования должно быть определено сос­тояние устройства обслуживания: может ли требование быть обслужено немедленно или его необходимо поместить в конец очереди. После завершения обслуживания тре­бования, исходя из числа требований в очереди, определяется, будет устройство обслу­живания свободно или же начнет обслуживание первого требования в очереди. Чтобы вычислить задержку требования в очереди, необходимо установить время его поступле­ния, так как задержка равна времени начала обслуживания требования (которое будет известно) минус время его поступления.

В этой системе есть два типа событий: поступ­ление требования и завершение обслуживания требования, приводящее к его уходу.

Динамическая природа дискретно-событийных имитационных моделей требует, что­бы мы следили за текущим значением имитационного времени по мере функциони­рования имитационной модели. Нам необходим также механизм для продвижения имитационного времени от одного значения к другому.

В имитационной модели пе­ременная, обеспечивающая текущее значение модельного времени, называется часами модельного времени. Существует два основных подхода к продвижению модельного времени: про­движение времени от события к событию и продвижение времени с постоянным шагом. Первый подход используется всеми основными имитационны­ми программами и большинством разработчиков, создающих свои модели на уни­версальных языках. Мы будем также использовать подход, при котором происходит продвижение времени от события к собы­тию.

При использовании продвижения времени от события к событию часы модель­ного времени в исходном состоянии устанавливаются в 0 и определяется время возникновения будущих событий. После этого часы модельного времени переходят на время возникновения ближайшего события, и в этот момент обновляются со­стояние системы с учетом произошедшего события, а также сведения о времени возникновения будущих событий. Затем часы модельного времени продвигаются ко времени возникновения следующего (нового) ближайшего события, обновля­ется состояние системы и определяется время будущих событий, и т. д.

Процесс продвижения модельного времени от времени возникновения одного события ко времени возникновения другого продолжается до тех пор, пока не будет выполне­но какое-либо условие останова, указанное заранее. Поскольку в дискретно-собы­тийной имитационной модели все изменения происходят только во время возник­новения событий, периоды бездействия системы просто пропускаются, и часы переводятся со времени возникновения одного события на время возникновения другого. (При продвижении времени с постоянным шагом такие периоды бездей­ствия не пропускаются, что приводит к большим затратам компьютерного време­ни.) Следует отметить, что длительность интервала продви­жения модельного времени от одного события к другому может быть различной.

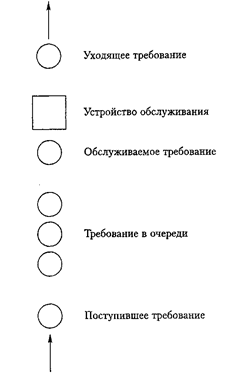Рассмотрим систему массового обслуживания с одним устройством (см. рис.).

В этой системе интервалы времени между поступлением требований А₁, А₂, ... явля­ются независимыми и одинаково распределенными случайными величинами. Когда требование поступает, а устройство свободно, обслуживание начинается немедленно. Время обслуживания S₁, S₂, ... следующих требований представлено независимыми оди­наково распределенными случайными величинами, на которые не влияют интерва­лы времени обслуживания. Если при поступлении требования устройство занято, требование становится в очередь. По завершении обслуживания требования уст­ройство выбирает требование из очереди (если такая имеется) по принципу FIFO (First In – First Out - «первым пришел - первым обслужен»).

Моделирование начинается с состояния «пустая и незанятая», то есть, когда в системе нет требований, и устройство обслуживания свободно.

С момента вре­мени, равного 0, мы начинаем ожидать поступление первого требования. Скорее всего, это произойдет по истечении первого интервала времени между поступле­ниями А₁ а не в момент времени, равный 0 (это было бы возможное, но особое предположение моделирования). Мы будем продолжать моделирование до тех пор, пока для определенного числа требований n не истечет время задержки в очереди, то есть моделирование прекратится, когда n-е требование будет обслу­жено. Следовательно, время завершения моделирования является случайной вели­чиной, которая зависит от наблюдаемых значений случайных переменных, обоз­начающих время между поступлениями требований и время обслуживания.

Для того чтобы определить критерии оценки работы системы, обратимся к трем параметрам их характеристики. Прежде всего, найдем ожидаемую среднюю за­держку в очереди для каждого из n требований, завершивших свое ожидание во время моделирования; эту величину обозначим как d(n). Слово «ожидаемая» в оп­ределении d(n) означает, что при заданном прогоне имитационной модели (или при заданном прогоне действительной системы, которую представляет имитаци­онная модель) средняя задержка, наблюдаемая для n-то числа требований, зависит от полученных наблюдений случайных переменных, обозначающих время между поступлениями требований и время обслуживания. При следующем прогоне ими­тационной модели (или на второй день — с реальной системой) требования будут прибывать в другие моменты времени, и необходимое время обслуживания также будет иным. Это приведет к получению другого среднего значения задержки для n требований. Следовательно, при прогоне имитационной модели среднее значение задержки требования в очереди также считается случайной величиной. Нам же необходимо установить ожидаемое значение случайной величины. Согласно од­ной интерпретации d(n) является средним огромного (фактически бесконечного) числа средних задержек в очереди n-го числа требований. После одного прогона имитационной модели, при котором зафиксированы задержки требований в оче­реди D₁, D₂,..., D_n, очевидной оценкой d(n) является формула

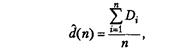
представляющая среднее время D_i n-то числа задержек, которое наблюдалось при моделировании.

Другим критерием в нашей простой системе является ожидаемое среднее число требований в очереди (без учета уже находящихся на обслуживании), обозначенное как q(n), где n указывает, что среднее вычисляется за период времени, который необходим для наблюдения n-го числа задержек, определяющих правило останова. Таким образом, нам нужно определить среднее по времени число требований в очереди. С этой целью число требований в момент времени t (для любого вещественного числа t ³ 0) мы обозначим как Q(t), а время, необходи­мое для наблюдения n-то числа задержек в очереди, как Т(n). Тогда для любого времени t между 0 и Т(n) значение Q(t) будет неотрицательным целым числом. Да­лее, пусть р_i - ожидаемая часть (имеющая значение от 0 до 1) времени, когда Q(t) равно i, тогда приемлемым определением q(n) будет

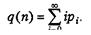
Таким образом, q(t) является взвешенным средним возможных значений i для очереди длиной Q(t), при этом весовые коэффициенты являются ожидаемой час­тью времени, которое расходуется на каждую из своих возможных длин очереди. Чтобы определить q(n), заменяем значения р_i их оценками и получаем

где р_i является частью времени, измеряемой (а не ожидаемой) в процессе модели­рования, когда число требований в очереди равнялось i. Однако для вычисления q(n) удобнее переписать формулу, используя некоторые геометрические методы. Пусть Т_i будет суммарным временем в течение моделирования очереди длиной i, тогда Т(n) = T₀ + T₁ + Т₂ +... и р_i = T_i/T(n). В результате приведенное выше уравне­ние (1.1) мы можем переписать как

На рис. 1 показано возможное течение времени или реализация Q(t) в систе­ме при условии, что n = 6 (на данном этапе не следует учитывать штриховку пря­моугольников). Требования прибывают в моменты времени, равные 0,4; 1,6; 2,1; 3,8; 4,0; 5,6; 5,8 и 7,2. Уход требований (завершение обслуживания) происходит в моменты времени, равные 2,4; 3,1; 3,3; 4,9 и 8,6. В момент времени, когда T(6)=8,6, моделирование завершается.

Обращаясь к рис. 1, имейте в виду, что Q(t) не учитывает требование, находя­щееся на обслуживании (если таковое есть), и в период времени между 0,4 и 1,6 очередь будет отсутствовать (Q(t)= 0), хотя при этом одно требование находится на обслуживании.

Чтобы вычислить значение q(n), вначале необходимо вычислить значения T_i, которые, прибегнув к помощи рис. 1, можно трактовать как интервалы времени (иногда отделенные друг от друга некоторым промежутком времени), в течение которых Q(t) равно 0, 1, 2 и т. д.:

T₀= (1,6 - 0,0) + (4,0 - 3,1) + (5,6 - 4,9) = 3,2;

Т₁= (2,1 - 1,6) + (3,1 - 2,4) + (4,9 - 4,0) + (5,8 - 5,6) = 2,3;

Т₂ = (2,4 - 2,1) + (7,2 - 5,8) = 1,7;

T₃=(8,6-7,2) = 1,4.

(Т_i = 0, когда i ³4, поскольку в данной реализации очередь никогда не достигает та­кой длины.) Числитель в уравнении (1.2)

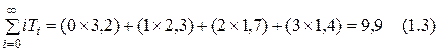
Рис. 1. Q(t), время поступления и время ухода в реализации системы массового обслуживания с одним устройством обслуживания

Отсюда оценка среднего по времени числа требований в очереди при данном прогоне имитационной модели q(6)=9,9/8,6=1,15. Каждый из не равных нулю членов в левой части формулы (1.3) соответствует заштрихованной площади рис 1. 1x2,3 соответствует площади, заштрихованной диагональными линиями (в четырех прямоугольниках), 2x1,7 - площади, заштрихованной перекрест­ными диагональными линиями (в двух прямоугольниках), 3x1,4 – затемненной площади (один прямоугольник).

Иными словами, суммирование в числителе урав­нения (1.2) представляет накопленную площадь под кривой Q(t) между началом и концом моделирования. С учетом того, что площадь под кривой является инте­гралом, мы можем написать следующее уравнение:

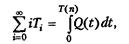
а оценка q(n) может быть выражена как

Выражения (1.4) и (1.2) эквивалентны для q(n), однако (1.4) предпочтитель­нее, поскольку интеграл в нем может быть рассчитан как накопление простых пло­щадей прямоугольников, возникающих в течение времени моделирования, что ме­нее удобно при явном суммировании по формуле (1.2). Более того, выражение (1.4) предполагает среднее для непрерывного Q(t), так как операцию интегрирова­ния можно только приблизительно считать непрерывным суммированием.

Третий выходной критерий оценки работы системы — показатель занятости устройства. Ожидаемый коэффициент использования устройства является отно­шением времени, когда устройство находится в состоянии занятости, ко времени моделирования (от 0 до Т(n)) и, следовательно, является числом между 0 и 1. Обо­значим его как u(n). При одной реализации моделирования оценкой u(n) является й(п), равная измеряемому отношению времени, когда устройство находится в со­стоянии занятости, ко времени моделирования. Теперь и(п) можно вычислить не­посредственно при моделировании, отметив моменты времени, когда меняются состояния устройства (со свободного на занятое, и наоборот), а затем выполнив соответствующие действия с вычитанием и делением. Однако такую величину удобнее рассматривать как среднее для непрерывного времени, подобное средней длине очереди, определив функцию занятости как

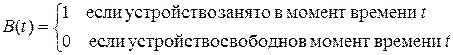
Таким образом, коэффициент й(п) можно выразить как часть времени, когда B(t) = 1. На рис. 2 изображен график функции B(t) для реализации процесса мо­делирования, использованного на рис. 1. В этом случае получаем

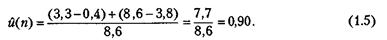
Результат указывает на то, что в ходе моделирования 90 % времени устройство за­нято. Но числитель в формуле (1.5) может также рассматриваться как площадь под функцией B(t), так как высота B(t) всегда равна либо 0, либо 1. Следовательно,

и мы снова видим, что й(п) является для непрерывной функции B(t) средним, со­ответствующим нашему понятию занятости. Как и в случае с q(n), коэффициент и(n) удобнее выражать через интеграл уравнения (1.6), поскольку в ходе модели­рования интеграл функции B(t) легче вычислять путем сложения площадей пря­моугольников. Для многих случаев моделирования, включающих разные устрой­ства обслуживания, статистика коэффициента использования дает достаточно информации для решения проблем нехватки ресурсов (коэффициент использова­ния, равный 100 %, связан с большими перегрузками показателей продвижения очереди) или их избытка (низкая занятость). Это особенно касается случаев, ког­да устройствами обслуживания являются такие дорогие приборы, как роботы про­изводственных систем или большие компьютеры (мэйнфреймы), задействован­ные в операциях по обработке данных.

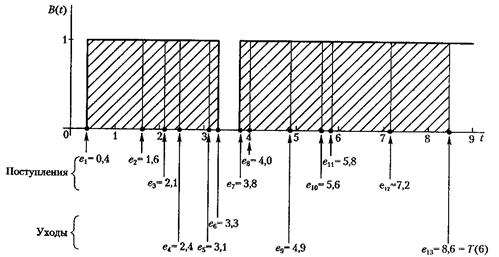
Рис. 2. B(t), время поступления и время ухода в реализации системы массового обслуживания с одним устройством обслуживания (та же реализация, что на рис. 1)

Итак, три критерия оценки работы системы включают: среднюю задержку в оче­реди d(n), среднее по времени число требований в очереди q(п); часть времени, когда устройство обслуживания находится в состоянии занятости u(n).

Средняя задержка требования в очереди является статистикой дискретного времени, по­скольку она определяется относительно ряда случайных переменных {D_i}, кото­рые имеют индекс дискретного времени i=1, 2, ....

Среднее по времени число тре­бований в очереди и часть времени, когда устройство обслуживания находится в состоянии занятости, - это примеры статистики непрерывного времени, по­скольку они определяются относительно совокупности случайных переменных {Q(t)} и {B(t)} соответственно, каждая из которых индексируется по параметру не­прерывного времени tÎ[0, ¥). (Символ Î означает «содержащийся». Таким обра­зом, в этом случае t может быть любым не отрицательным вещественным числом.)

Как статистика дискретного времени, так и статистика непрерывного времени часто используются в моделировании, при этом они позволяют получить не толь­ко средние показатели. Например, нам могут понадобиться значения либо макси­мальной наблюдаемой задержки в очереди (статистика дискретного времени), ли­бо части времени в ходе моделирования, когда в очереди насчитывалось, как минимум, пять требований (статистика непрерывного времени).

Дата добавления: 2014-12-09; просмотров: 480; Нарушение авторских прав

Мы поможем в написании ваших работ!