Экстремум функции

ТЕМА 5. ЗАДАЧИ ОПТИМИЗАЦИИ: ОДНОФАКТОРНЫЕ ПРОИЗВОДСТВЕННЫЕ ФУНКЦИИ.

Основные понятия оптимизации

Деятельность отдельных людей и коллективов, как правило, связана с выбором таких решений, которые позволили бы получить некие оптимальные результаты - затратить минимум средств на питание семьи, достичь максимальной прибыли предприятий, добиться наилучших показателей в спорте и т. д. Но в каждой конкретной ситуации надо считаться с реальными условиями задачи.

При расчете затрат на питание следует приобрести те продукты и в таком количестве, чтобы организм получил необходимые ему жиры, белки, углеводы и т. д. Предприятие не сможет обеспечить максимальную прибыль без учета реальных запасов сырья, его стоимости и целого ряда других факторов. Для достижения наилучших показателей в спорте необходимо правильно организовать тренировку спортсменов, оптимально использовать имеющиеся технические средства и площадки, правильно сформировать команду.

Под оптимизацией понимают процесс выбора наилучшего варианта решения из всех возможных. В процессе решения задачи оптимизации обычно необходимо найти оптимальные значения некоторых параметров, определяющих данную задачу (это управляющие параметр –- проектные параметры – в экономических задачах – параметры плана).

Число n -этих параметров 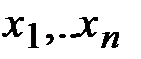характеризует размерность (и степень сложности) задачи оптимизации. Варьирование (изменении) этих параметров допускается в некоторых пределах, определяемых технологическими особенностями производства, ресурсами или физическими законами – т.е. на параметры налагаются некоторые условия – это условия- ограничения. Выбор оптимального решения или сравнение двух альтернативных решений производится с помощью некоторой зависимой величины (функции), определяемой управляющими параметрами. Эта величина называется целевой функцией (критерием качества).

Примеры:

1). Рассмотрим одну из старинных русских задач: сколько надо взять бабуле для продажи на рынке живых гусей, уток и кур, чтобы она получила наибольшую выручку, если производитель может доставить на рынок птицы массой не более P кг.

При этом вес одного гуся, утки и курицы, а также их стоимость заданы.

2) Задача питания: какое количество и каких продуктов необходимо купить хозяйке, чтобы затратить на покупку минимум денег и одновременно обеспечить для организма необходимое количество жиров, белков, углеводов и т. д. Стоимость продуктов и количество жиров. белков, углеводов и других компонентов в каждом продукте известны.

3) Еще пример: какую продукцию и в каком количестве следует выпустить предприятию с учетом имеющихся у предприятия ресурсов и материалов, чтобы получить наибольшую прибыль. Прибыль, которую приносит каждый вид продукции и затраты ресурсов и материалов на выпуск единицы продукции каждого вида считаются заданными.

Во всех этих задачах можно выделить достигаемую при решении задачи цель(сформулировать целевую функцию или оптимизационный критерий).

1. минимум затрат на питание;

2. максимум выручки за проданную птицу;

3. максимум прибыли предприятия;

а также условия, ограничивающие возможные значения неизвестных (условия- ограничения):

1) необходимое для организма количество жиров, белков и углеводов;

2) массу птицы P, которую продавец может доставить на рынок;

3) количество ресурсов и материалов, которыми располагает предприятие

Для того, чтобы что-то рассчитать, надо формализовать задачу, т. е. составить математическую модель, поскольку по своей природе математические методы можно применять не непосредственно к изучаемой действительности, а лишь к математическим моделям тех или иных явлений. Причем результаты исследований математических моделей представляют практический интерес только тогда, когда модели адекватно отображают реальные ситуации и достаточно совершенны.

В приведенных выше задачах требовалось отыскать максимум или минимум некоторой целевой функции 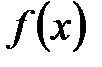. Но задача отыскания минимума функции эквивалентна задаче отыскания максимума той же функции, взятой со знаком минус, и наоборот. Поэтому будем говорить об оптимальном (optimum- наилучший) значение целевых функций.

Математические модели оптимизационных задач.

В наиболее общем смысле теория оптимизации представляет собой совокупность фундаментальных математических результатов и численных методов, ориентированных на нахождение и идентификацию наилучших вариантов из множества альтернатив и позволяющих избежать полного перебора и оценивания возможных вариантов.

Процесс оптимизации лежит в основе всей экономической деятельности, поскольку классические функции экономиста заключаются в том, чтобы, с одной стороны, проектировать новые, более эффективные и менее дорогостоящие экономические системы и, с другой стороны, разрабатывать методы повышения качества функционирования существующих систем.

Для того чтобы использовать математические результаты и численные методы теории оптимизации для решения конкретных экономических задач, необходимо:

а) установить границы подлежащей оптимизации системы;

б) определить количественный критерий, на основе которого можно произвести анализ вариантов с целью выявления "наилучшего";

в) осуществить выбор внутрисистемных переменных, которые используются для определения характеристик и идентификации вариантов;

г) построить модель, отражающую взаимосвязи между переменными.

Эта последовательность действий составляет содержание процесса постановки задачи экономической оптимизации. Корректная постановка задачи служит ключом к успеху оптимизационного исследования и ассоциируется в большей степени с искусством, нежели с точной наукой.

Рассмотрим вышеперечисленные пункты подробнее.

а) Определение границы изучаемой системы. Прежде чем приступить к оптимизационному исследованию, важно четко определить границы изучаемой системы. В данном контексте система предстает как некоторая изолированная часть реального мира. Границы системы задаются пределами, отделяющими систему от внешней среды, и служат для выделения системы из ее окружения. При проведении анализа обычно предполагается, что взаимосвязи между системой и внешней средой зафиксированы на некотором выбранном уровне представления. Тем не менее, поскольку такие взаимосвязи всегда существуют, определение границ системы является первым шагом в процессе приближенного описания реальной системы.

б) Характеристический критерий.Если подлежащая исследованию система определена и ее границы установлены, то на следующем этапе постановки задачи оптимизации необходимо осуществить выбор критерия, на основе которого можно оценить характеристики системы, с тем чтобы выявить "наилучший" проект или множество "наилучших" условий функционирования системы. Независимо от того, какой критерий выбирается при оптимизации, "наилучшему" варианту всегда соответствует минимальное (или максимальное) значение характеристического показателя качества функционирования системы.

Важно отметить также, что только один критерий может использоваться при определении оптимума, так как невозможно получить решение, которое, например, одновременно обеспечивает минимум затрат, максимум надежности и минимум потребляемой энергии. Здесь мы сталкиваемся с существенным упрощением реальной ситуации, поскольку в ряде практических случаев было бы весьма желательно найти решение, которое бы являлось "наилучшим" с позиций нескольких различных критериев.

в) Независимые переменные. Эти переменные должны адекватно описывать допустимые проекты или условия функционирования системы. В процессе выбора независимых переменных следует принять во внимание ряд важных обстоятельств.

Во-первых, необходимо провести различие между переменными, значения которых могут изменяться в достаточно широком диапазоне, и переменными, значения которых фиксированы и определяются внешними факторами.

Во-вторых, при постановке задачи следует учитывать все основные переменные, которые влияют на функционирование системы.

При выборе независимых переменных целесообразно руководствоваться правилом, согласно которому следует рассматривать только те переменные, которые оказывают существенное влияние на характеристический критерий, выбранный для анализа сложной системы.

г) Модель системы.После выполнения вышеперечисленных этапов необходимо построить модель, которая описывает взаимосвязи между переменными задачи и отражает влияние независимых переменных на степень достижения цели, определяемой характеристическим критерием.

Математической моделью оптимизационной задачи называется совокупность математических соотношений, представляющие собой равенства или неравенства, связывающие переменные и описывающие условия задачи и определяющие критерий эффективности.

Таким образом, в самом общем представлении структура модели включает основные уравнения материальных и энергетических балансов, соотношения, связанные с проектными решениями, а также уравнения, описывающие физические процессы, протекающие в системе. Эти уравнения обычно дополняются неравенствами, которые определяют область допустимых значений независимых переменных, позволяют определить требования, накладываемые на верхние или нижние границы изменения характеристик функционирования системы, и установить лимиты имеющихся ресурсов.

Из вышеизложенного следует, что задача в виде, пригодном для применения оптимизационных методов, объединяет характеристическую меру, множество независимых переменных и модель, отражающую взаимосвязь переменных. Поскольку требования, предъявляемые к оптимизационным задачам, являются весьма общими и носят абстрактный характер, область приложения методов оптимизации является достаточно широкой.

д) Примеры экономических и технологических критериев оптимальности.Для того чтобы выбрать показатель эффективности, т. е. целевую функцию, нужно прежде всего четко установить, какая цель достигается при реализации того или иного мероприятия. На нескольких примерах покажем, какие показатели можно принять за целевую функцию:

План снабжения предприятий. Задача состоит в обеспечении сырьем при минимальных расходах на перевозках. В данном случае за показатель эффективности (целевую функцию) R целесообразно принять суммарные расходы на перевозку сырья за единицу времени ( ).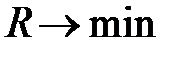

Постройка участка магистрали. Требуется так спланировать строительство, чтобы закончить его как можно скорее. Естественным показателем эффективности было бы время завершения стройки, если бы оно не было связано со случайными факторами (отказы техники, задержки в выполнении отдельных работ). Поэтому в качестве целевой функции можно выбрать среднее ожидаемое время T окончания стройки ( ).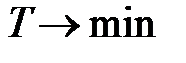

Продажа сезонных товаров. В качестве целевой функции можно взять среднюю ожидаемую прибыль P от реализации товаров за сезон ( ).

е) Постановка задачи оптимизации. Предполагается осуществить какое-либо мероприятие, преследующее определенную цель. Существуют какие-то условия, и в рамках этих условий требуется принять такое решение, чтобы мероприятие было в каком-то смысле наиболее выгодным.

Операцией называется всякое мероприятие (система действий), объединенное единым замыслом и направленное к достижению какой-то цели. Операция всегда есть управляемое мероприятие, т.е. от нас зависит, каким способом выбрать некоторые параметры, характеризующие ее организацию. Всякий выбор параметров называется решением. Оптимальным называется решение, являющееся по тем или иным признакам предпочтительней перед другими. Цель операции – предварительное количественное обоснование оптимальных решений. Те параметры, совокупность которых образует решение, называются элементами решения. Например, из пунктов перевозятся грузы в пункты . Пусть – количество грузов, которое будет перевезено из пункта i в пункт j. В этом случае будет элементом решения, а совокупность всех есть решение.

В любой задаче существуют условия, являющиеся ограничениями, например, грузоподъемность транспорта, количество груза в предыдущем примере. Совокупность условий определяет множество возможных решений X. И вопрос состоит в том, чтобы в множестве возможных решений X выделить те решения , которые с той или иной точки зрения эффективнее.

Для сравнения между собой по эффективности разные решения используется количественный критерий, называемый, как уже определялось выше, целевой функцией (или показателем эффективности).

"Лучшим" будет считаться то решение, которое в максимальной степени способствует достижению поставленной цели.

В наиболее сложных случаях, когда развитие операции и ее исход зависят от большого числа сложно переплетающихся между собой случайных факторов, аналитические методы вообще отказываются служить, применяются статистические методы моделирования.

Экстремум функции.

Часто при реализации какого-нибудь мероприятия имеет место ситуация, когда достижение цели можно осуществить различными способами (в дальнейшем условимся эти способы называть планами). Все такие планы называются допустимыми. В этом случае появляется возможность выбирать оптимальный в некотором смысле план. С математической точки зрения оптимальность некоторого плана означает, что этот план экстремизирует (максимизирует или минимизирует) некоторую функцию на множестве допустимых планов.

Математическое программирование представляет собой математическую дисциплину, занимающуюся изучением экстремальных задач и разработкой методов их решения.

Прежде чем приступим к изложению методов решения задач математического программирования, кратко дадим сведения, относящиеся к отысканию экстремума функции.

Как известно, решение многих теоретических и практических задач сводится к отысканию экстремума (наибольшего или наименьшего значения) функции 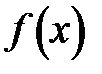n-мерного векторного аргумента x,и определение экстремума функции является одной из основных задач классического математического анализа. Оптимизируемая функция 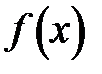есть целевая функция или критерий оптимальности. Вектор , доставляющий экстремум целевой функции, называют оптимальным (выше мы вводили для него определение оптимальный план). Если – точка минимума функции , то для функции она является точкой максимума, так как графики функций и симметричны относительно оси абсцисс. Таким образом, минимум функции 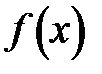и максимум функции – 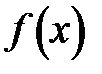достигаются при одном и том же значении переменной поэтому .

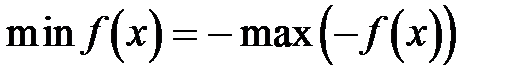Рассуждая аналогично, этот вывод нетрудно распространить на случай многих переменных ; экстремальные значения этих функций достигаются при одних и тех же значениях переменных.

Экстремум функции может иметь глобальный или локальный характер, в свою очередь, глобальный экстремум может быть строгим или нестрогим. На примере минимума функции одной переменной раскроем эти понятия.

Говорят, что точка доставляет глобальный минимум функции одной переменной 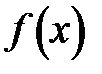на множестве X, если при некотором достаточно малом для всех (x принадлежат X), удовлетворяющих условию , выполняется неравенство 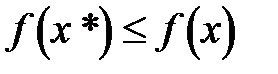. Если при этом это неравенство выполняется как строгое, то точка называется точкой строгого глобального минимума (рис. 4.1, а), если же в выражении 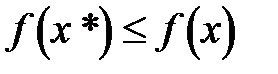равенство возможно при , то реализуется нестрогий минимум (на рис. 5.1, б диапазон изменений x, на котором реализуется нестрогий минимум, на оси абсцисс выделен).

Минимум, определенный только на ограниченном отрезке, называется локальным минимумом.

Все определения для максимума получаются заменой знаков предыдущих неравенств на обратные.

На рис. 4.2 показаны экстремумы функции одной переменной 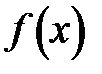на отрезке [a, b]. Здесь 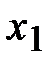, , 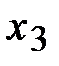– точки локального максимума, а 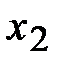, – локального минимума. В точке 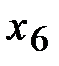реализуется глобальный максимум, а в точке 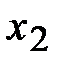– глобальный минимум.

а) б)

=

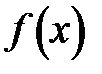
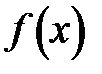
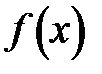O x O x

Рис. 5.1. Глобальный минимум: а – строгий; б – нестрогий

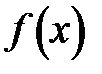
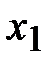
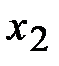
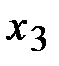
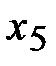
O a 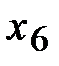b x

Рис. 5.2. Экстремумы функции

Простейшей и вместе с тем типичной задачей является задача определения экстремума функции, когда переменные могут изменяться во всем пространстве без всяких ограничений. Если при этом функция будет непрерывно дифференцируемая, то экстремальными будут те значения переменных, при которых обращаются в нуль все частные производные экстремизируемой функции. Такую задачу называют задачей безусловной оптимизации.

Однако на практике встречаются задачи, когда на область изменения переменных накладываются ограничения, выражаемые условиями как в виде равенств, так и неравенств. В этом случае говорят, что имеет место задача условной оптимизации. (В частности, при составлении экономических планов приходится учитывать ограничения типа “потребность в данном продукте не превосходит такой-то величины. Подобные ограничения могут налагаться на факторы при составлении, например, математических моделей физических процессов.) Такие условия в классическом математическом анализе не рассматриваются, а изучается задача экстремизации функции при условиях, имеющих вид только равенств.

То, что для решения задачи с ограничениями нужны новые методы, можно показать на следующем примере.

Пусть дана линейная функция одной переменной 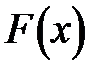= x и требуется найти экстремум (минимум или максимум) этой функции.

Как известно, при отсутствии ограничений на область изменения переменных, определение экстремума сводится к определению такой точки, где производная функции обращается в нуль. В нашем примере производная функции нигде не обращается в нуль, так как .

Теперь определим область изменения переменных неравенствам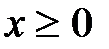и и 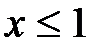(рис. 5.3). Как видим, в этом случае та же функция уже имеет максимум в точке x = 1 и минимум в точке x = 0.

= x

0 1 x

Рис. 5.3. Определение экстремума функции при задании ограничений на область изменения переменной

В тех случаях, когда имеет место экстремум при наличии дополнительных ограничений на область изменения переменных, говорят, что функция имеет условный экстремум. В нашем примере экстремумы функции как раз и являются условными. Изучением задач об условном экстремуме функции в различных их постановках и разработкой методов их решения занимается математическая дисциплина, которая называется математическое программирование.

Понятие условного экстремума распространяется и на случай, когда функция зависит от многих переменных. Поэтому в общем виде математическая постановка экстремальной задачи состоит в следующем:

Определить наибольшее или наименьшее значение целевой функции

(5.1)

при условиях:

, , (5.2)

где f и 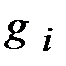– заданные функции, а 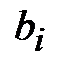– некоторые действительные числа.

Дата добавления: 2014-12-09; просмотров: 648; Нарушение авторских прав

Мы поможем в написании ваших работ!