Комплексное число

1)Комплексным числом z называеться выражение вида z=a+bi ,где a и b действительные чила ,а i мнимая ед,i²= -i

2)Мнимая единица — обычно комплексное число, квадрат которого равен отрицательной единице.

3)

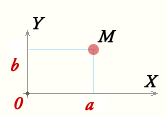Любое комплексное число a=a+bi можно изобразить точкой M(a;b) на плоскости Оху такой ,что a=Rez и b=jmz i=(0;1)-вектор

1.Плоскость ,на которой изображаются комплексные чила ,наз комплексной плоскостью

2.Ось обцисс называеться осью действия

3. Оь ординатная наз мнимой осью

4)

Аргументом комплексного числа z = a + ib (z ≠ 0) называется величина угла между положительным направлением действительной оси и вектором величина угла считается положительной, если угол отсчитывается против часовой стрелки, и отрицательным в противном случае.

5)Действия с комплексными числами, заданных в тригонометрической форме

Запись комплексного числа z = a + bi в виде z=rcos+isin называется тригонометрической формой комплексного числа.

Модуль комплексного числа: r²=a²+b²

Аргумент комплексного числа:

cosx=a/r sinx=b/r

6)

1-ое свойство

При умножении степеней с одинаковыми основаниями

показатели складываются, а основание остается неизменным.

если a — любое число, а n и k — натуральные числа то:

a ⁿ • a ^k = a ^n+k

2-ое свойство

При делении степеней с одинаковыми основаниями

показатели вычитаются, а основание остается неизменным.

если a ≠ 0, а n и k — натуральные числа и n > k то:

a ⁿ/a ^k= a ^n−k

Исходя из этого легко запомнить, что если

a ≠ 0, то a 0 = 1

3-е свойство

При возведении степени в степень показатели перемножаются.

если a — любое число, а n и k — натуральные числа то:

(a ⁿ) ^k = a ^nk

7)Пусть дано положительное число a и произвольное действительное число n. Число an называется степенью, число a — основанием степени, число n — показателем степени.

По определению полагают:

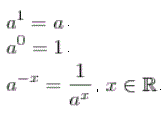
Если a и b — положительные числа, x и y — любые действительные числа, то справедливы следующие свойства:

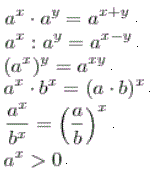
8)Определение логарифма

Логарифмом числа b по основанию а называется показатель степени, в которую нужно возвести а, чтобы получить b.

Десятичные логарифмы (логарифмы по основанию 10)log₁₀a обозначаются как lga

9) свойства логарифмов:

1. Если а>1,то для х>1 log_ax>0 и для 0<x<1 log_ax>0

2. Если 0<a<1 ,то для x>1 log_ax<0 и для 0<x<1 log_ax>0

3. Если a>0,а≠1,то log_a1=0

4.Если a>0, a≠1, то log_aa=1

5.Если х₁=х₂ ,то log_ax₁ =log_ax₂,a>0,a≠1

6. Логарифм произведения равен сумме логарифмов сомножителей:

log_a(x₁*x₂)=log_ax₁+log_ax₂ ; a>0 ,a≠1 ,x₁>0 x₂>0

7. Логарифм lчастичного равен разности логарифмов делимого и делителя:

log_a(x₁/x₂)=log_ax₁-log_ax₂ ; a>0 ,a≠1,x₁>0 x₂>0

8.Логарифм степени равен логарифму основания ,умноженному на показатель степени:

log_ax^b=b log_ax ;a>0,a≠1,a>0

9. Формула перехода к новому основанию:

log_ax=(log_bx/log_ba) ; a>0 ,a≠1 ,b>0 ,b≠1, x>0

log_ab*log_ba=1

10. Значение логарифма не изменится,если чило,от которого берется логарифм,и основние логарифма возвести в одну и ту же вещественную степень log_ax=log_a^kx^k

10)Радиан-центральный угол,длина которого равна радиусу,Обозначаеться 1 рад. 1рад=180/n, причем 1рад=57,

1=n/180 paд.

полный угол равен 2n радиан

11)

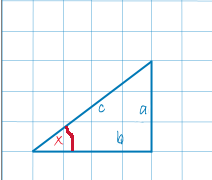
sinx-Это отношение противолежащего катета к гипотенузе:

sinx = а/с

cosx-Это отношение прилежащего катета к гипотенузе:

сosx= в/с

tgx-Это отношение противолежащего катета к прилежащему:

tgx = а/в

ctg-Это отношение прилежащего катета к противолежащему:

ctgx = в/а

12)Основные тригонометрические соотношения связаны тождествами:

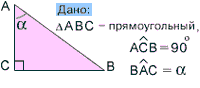
1) tg a = sin a /cos a

2) sin2 a + cos2 a = 1

3) 1 + tg2 a = 1/cos2 a

4) 1 + 1/tg2 a = 1/sin2 a

5) sin(90o– a ) = cos a

6) cos(90o– a ) = sin a

13)Формулы двойного аргумента

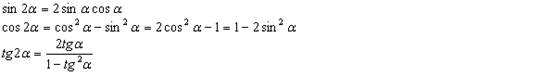
14)arcsin числа а называется угол из отрезка , синус которого равен числу а.

arccos числа а называется угол из отрезка , косинус которого равен числу а.

arctg числа а называется угол из интервала , тангенс которого равен числу а.

arcctg числа а называется угол из интервала , котангенс которого равен числу а.

Дата добавления: 2014-12-09; просмотров: 387; Нарушение авторских прав

Мы поможем в написании ваших работ!