Оценивание погрешности при косвенных измерениях

При косвенных измерениях искомое значение величины находят расчетом на основе прямых измерений других физических величин, функционально связанных с искомой величиной известной зависимостью

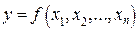(1.1)

где 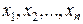– подлежащие прямым измерениям аргументы функции .

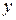Результатом косвенного измерения является оценка величины у, которую находят подстановкой в формулу (1.1) измеренных значений аргументов х_i .

Поскольку каждый из аргументов х_i измеряется с некоторой погрешностью, то задача оценивания погрешности результата сводится к суммированию погрешностей измерения аргументов. Однако особенность косвенных измерений состоит в том, что вклад отдельных погрешностей измерения аргументов в погрешность результата зависит от вида функции (1.1).

Для оценки погрешностей существенным является разделение косвенных измерений на линейные и нелинейные косвенные измерения.

При линейных косвенных измерениях уравнение измерений имеет вид:

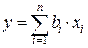, (1.2)

где 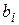– постоянные коэффициенты при аргументах х_i .

Результат линейного косвенного измерения вычисляют по формуле (1.2), подставляя в неё измеренные значения аргументов.

Погрешности измерения аргументов х_i могут быть заданы своими границами .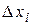

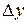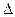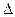При малом числе аргументов (меньше пяти) простая оценка погрешности результата получается простым суммированием предельных погрешностей (без учета знака), т.е. подстановкой границ х₁, х₂,…, 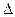х_n в выражение:

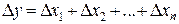. (1.3)

Однако эта оценка является излишне завышенной, поскольку такое суммирование фактически означает, что погрешности измерения всех аргументов одновременно имеют максимальное значение и совпадают по знаку. Вероятность такого совпадения практически равна нулю. Для нахождения более реалистичной оценки переходят к статическому суммированию погрешности аргументов по формуле:

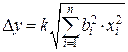, (1.4)

где 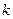– коэффициент, определяемый принятой доверительной вероятностью (при Р= 0,9 при k = 1,0; Р = 0,95 при k = 1,1; Р= 0,99 при k = 1,4).

Нелинейные косвенные измерения – любые другие функциональные зависимости, отличные от (1.2).

При сложной функции (1.1) и, в особенности, если это функция нескольких аргументов, определение закона распределения погрешности результата связано со значительными математическими трудностями. Поэтому в основе приближенного оценивания погрешности нелинейных косвенных измерений лежит линеаризация функции (1.1) и дальнейшая обработка результатов, как при линейных измерениях.

Запишем выражение для полного дифференциала функции у через частные производные по аргументам х_i:

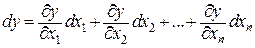. (1.5)

По определению полный дифференциал функции – это приращение функции, вызванное малыми приращениями её аргументов.

Учитывая, что погрешности измерения аргументов всегда являются малыми величинами по сравнению с номинальными значениями аргументов, можно заменить в формуле (1.5) дифференциалы аргументов 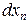на погрешность измерений 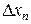, а дифференциал функции 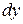на погрешность результата измерения :

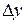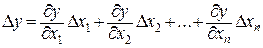. (1.6)

Если проанализировать формулу (1.6), то можно получить простые правила оценивания погрешности результата нелинейного косвенного измерения:

- если результат измерений получается перемножением измерений 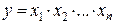или делений измерений 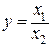, то для получения полной относительной погрешности складываются относительные погрешности каждого измерения 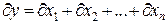, где ;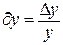

- если результат измерений получается суммирование измерений 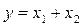или вычитанием измерений 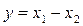, то для получения полной погрешности складываются абсолютные погрешности каждого измерения ;

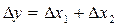- если результат измерений возведен в степень, то для получения полной относительной погрешности показатель степени умножается на относительную погрешность измерения.

Дата добавления: 2015-06-30; просмотров: 267; Нарушение авторских прав

Мы поможем в написании ваших работ!