Оценивание неопределенности измерений

В соответствии с РМГ 43неопределенность измерений -параметр, связанный с результатом измерений и характеризующий рассеяние значений, которые могли бы быть обоснованно приписаны измеряемой величине.

Неопределенность результата измерения отражает отсутствие точного значения измеряемой величины, т.е. переменной. Результат измерения поправки на известные систематические эффекты все еще является только оценкой значения измеряемой величины, вследствие неопределенности, возникающей из-за случайных эффектов и неточной поправки результата на систематические эффекты. Результат измерения (после внесения поправки) может быть (неизвестно на сколько) очень близким к значению измеряемой величины, т.е. может иметь пренебрежимо малую погрешность, даже если он может иметь большую неопределенность. На практике существуют всевозможные источники неопределенности измерения, такие как:

- неполное определение измеряемой величины;

- несовершенная реализация определения измеряемой величины;

- непрезентативная выборка, т.е. измеренный образец может не представлять измеряемую величину;

- неадекватное знание эффектов от условий окружающей среды, влияющих на измерение, или несовершенное измерение условий окружающей среды;

- субъективная систематическая ошибка оператора при снятии показаний аналоговых средств измерений;

- разрешающая способность или порог чувствительности средств измерений;

- неточные знания констант и других параметров, взятых из внешних источников и используемых при обработке данных и другие.

Основным количественным выражением неопределенности измерений является стандартная неопределенность u. Стандартная неопределенность измерений - неопределенность результата измерений, выраженная в виде среднего квадратического отклонения.

Различают два типа вычисления стандартной неопределенности:

- вычисление по типу А - путем статистического анализа результатов многократных измерений;

- вычисление по типу В - с использованием других источников информации об измеряемом значение.

Исходными данными для вычисления неопределенности по типу А 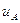являются результаты многократных измерений: 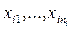(где ; 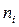- число измерений 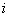-й входной величины).

Стандартную неопределенность единичного измерения 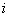-й входной величины вычисляют по формуле (1.7):

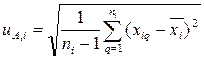, (1.7)

где 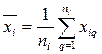- среднее арифметическое результатов измерений 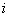-й входной величины.

Стандартную неопределенность 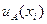измерений 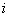-й входной величины, при которых результат определяют как среднее арифметическое, вычисляют по формуле 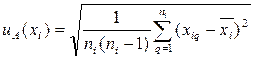(1.8):

(1.8)

В качестве исходных данных для вычисления неопределенности по типу В 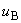используют:

- данные предшествовавших измерений величин, входящих в уравнение измерения; сведения о виде распределения вероятностей;

- данные, основанные на опыте исследователя или общих знаниях о поведении и свойствах соответствующих приборов и материалов;

- неопределенности констант и справочных данных;

- данные поверки, калибровки, сведения изготовителя о приборе и т.п.

Неопределенности этих данных обычно представляют в виде границ отклонения значения величины от ее оценки. Наиболее распространенный способ формализации неполного знания о значении величины заключается в постулировании равномерного закона распределения возможных значений этой величины в указанных (нижней и верхней) границах [θ_i-,θ_i+] для 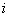-й входной величины. При этом стандартную неопределенность, вычисляемую по типу В - , определяют по формуле:

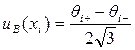, (1.9)

где θ_i - неисключенная систематическая погрешность, заданная границами ± θ.

а для симметричных границ (± θ_i) - по формуле:

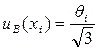, (1.10)

Примечание - В случае других законов распределения формулы для вычисления неопределенности по типу В будут иными.

Для вычисления коэффициента корреляции 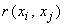используют согласованные пары измерений 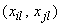(где 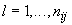; 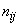- число согласованных пар результатов измерений):

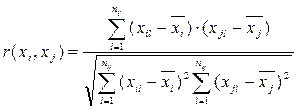(1.11)

В большинстве случаев измеряемая величина у не является прямо измеряемой, а зависит от других измеряемых величин 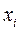, входящих в функциональную зависимость вида 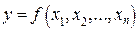или в модель F(x,y) = 0. Тогда суммарную неопределенность можно рассчитать используя следующие формулы:

- в случае отсутствии корреляции 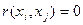оценок суммарная стандартная неопределенность 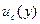определяется по формуле:

, (1.12)

где с_i = 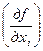- коэффициенты чувствительности;

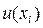- стандартная неопределенность 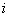-й входной величины, вычисленная по типу А или В.

- в случае коррелированных оценок 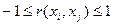суммарную стандартную неопределенность вычисляют по формуле:

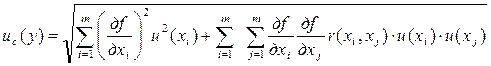(1.13)

где 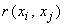- коэффициент корреляции;

- в случае положительно коррелированных оценок 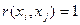суммарную стандартную неопределенность вычисляют по формуле:

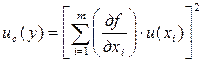(1.14)

- в случае 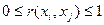и 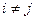суммарную стандартную неопределенность вычисляют по формуле:

(1.15)

Суммарная стандартная неопределенность может повсеместно использоваться для выражения неопределенности результата измерения, но в некоторых случаях в промышленности, торговле и регулирующих актах необходимо дать неопределенность в виде интервала для результата измерения, в пределах которого, можно ожидать, находится большая часть распределения значений, которые можно с достаточным основанием приписывать измеряемой величине. Из этого следует, что результатом измерения должен быть интервал, центром которого является искомое значение с данной вероятностью того, что в процессе повторных измерений оно будет находиться в пределах этого интервала. Такой интервал представляется с помощью расширенной неопределенности U. Значение расширенной неопределенности находиться по формуле:

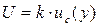, (1.16)

где - коэффициент охвата;

Если значения некоторой величины и ее стандартная неопределенность подчиняется нормальному закону распределения, то при числе степеней свободы 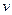= ∞ коэффициент охвата k равен 2 при вероятности Р = 0,95.

Если вычисление значений входных величин и соответствующих стандартных неопределенностей осуществляется по методу типа А, а количество измерений равно n, то данное вычисление значений ограничено числом степеней свободы 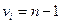, то тогда коэффициент охвата рассчитывается по формуле:

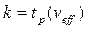, (1.17)

где 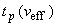- квантиль распределения Стьюдента с эффективным числом степеней свободы 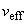и доверительной вероятностью Р;

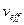- эффективная степень свободы, вычисляется по формуле:

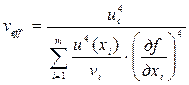(1.18)

Дата добавления: 2015-06-30; просмотров: 536; Нарушение авторских прав

Мы поможем в написании ваших работ!