Объяснение нового материала

Алгоритм решения логарифмических неравенств:

А) Найти область определения неравенства (подлогарифмическое выражение больше нуля).
Б) Представить (если возможно) левую и правую части неравенства в виде логарифмов по одному и тому же основанию.
В) Определить, возрастающей или убывающей является логарифмическая функция:

если t>1, то возрастающая; если 0<t>1, то убывающая.
Г) Перейти к более простому неравенству (подлогарифмических выражений), учитывая, что знак неравенства сохранится, если функция возрастает, и изменится, если она убывает

Решим неравенство такого вида log ₄ (2x+ 3) > log ₄ (x-5)

При решении логарифмического неравенства, на что вначале смотрим? (на основание)

-Какое здесь основание? (4>1, функция возрастает)

-Еще, что должны помнить? (подлогарифмическое значение должно быть больше нуля)

-Если основание больше единицы, то логарифмическое уравнение

log ₄ (2x+ 3) > log ₄ (x-5)

равносильно системе неравенств 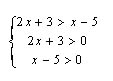так, как 4>1

-В математике всегда надо уметь видеть. Теперь, я хочу, чтобы вы увидели основной момент при переходе из логарифмического неравенства в систему неравенств.

В log₄ (2x+ 3)> log₄ (x-5), необходимо, чтобы 2х+3>0 и х-5>0. Если внимательно посмотрите в 2х+3 > х-5, то вы увидите, что если х-5 больше нуля, то тем более 2х+3 будет больше нуля.

Значит, достаточно написать только это неравенство х-5>0. Мы написали вначале это правильно, но теперь облегчаем себе работу при решении системы неравенств, так как мы решаем на одно неравенство меньше.

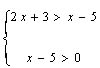
Перейдем от логарифмического неравенства к равносильной системе неравенств и решим ее.

x>-8

x>5

Ответ: (5;+∞)

В этом неравенстве вы видите: основание 0<a<1 функции убывает, поэтому знак меняем у неравенства f (x)<g(x),

так как f (x)<g(x), достаточно, чтоб f (x)>0.

Дата добавления: 2015-06-30; просмотров: 237; Нарушение авторских прав

Мы поможем в написании ваших работ!