
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Тема: Теорема Виета
1. Докажите, что уравнение
x3 + ax2 - b = 0,
где a и b вещественные и b > 0, имеет один и только один положительный корень.
2. При каких a и b уравнение x3 + ax + b = 0 имеет три различных решения, составляющих арифметическую прогрессию?
3. Докажите, что если x1, x2, x3 — корни уравнения x3 + px + q = 0, то
x22 + x2x3 + x32 = x12 + x1x3 + x32 = x12 + x1x2 + x22 = - p.
4. Пусть a, b и c — три различных числа. Решите систему
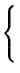
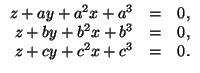
5. Автор: М.Ф.Безбородников
Какому условию должны удовлетворять коэффициенты a, b, c уравнения x3 + ax2 + bx + c, чтобы три его корня составляли арифметическую прогрессию?
Ответ
Ответ: Искомое соотношение: c=[ab/3]-[2/27]a3 (или, что то же самое, одни из корней должен равняться -[a/3]).
6. а) Известно, что
| x + y | = | u + v, |
| x2 + y2 | = | u2 + v2. |
Докажите, что при любом натуральном n выполняется равенство
xn + yn = un + vn.
б) Известно, что
| x + y + z | = | u + v + t, |
| x2 + y2 + z2 | = | u2 + v2 + t2, |
| x3 + y3 + z3 | = | u3 + v3 + t3. |
Докажите, что при любом натуральном n выполняется равенство
xn + yn + zn = un + vn + yn.
| <== предыдущая страница | | | следующая страница ==> |
| Теорема Банаха | | | Подсказка |
Дата добавления: 2015-06-30; просмотров: 288; Нарушение авторских прав

Мы поможем в написании ваших работ!