Решение. Рассмотрим многочлен P(x)=(x-a)(x-b)(x-c)

Рассмотрим многочлен P(x)=(x-a)(x-b)(x-c). Числа a, b, c - корни этого многочлена. Раскроем скобки и найдем коэффициенты этого многочлена: P(x)=(x-a)(x-b)(x-c)=x³-(a+b+c)x²+(ab+bc+ca)x-abc. (По существу, эта выкладка есть доказательство теоремы Виета для многочлена третьей степени). Таким образом, из условия следует, что P(x)=x³-px²+qx-r, где p, q, r - положительные числа. Если x - неположительное число, то каждое их слагаемых x³, -px², qx неположительно, следовательно, в этом случае P(x)<0. Итак, многочлен P(x) не имеет неположительных корней, т.е. его корни a, b, c - положительны, что и требовалось доказать.

12. Числа x, y, z удовлетворяют системе

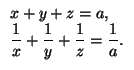
Докажите, что хотя бы одно из этих чисел равно a.

13. Дискриминант кубического уравнения. Пусть уравнение x³ + px + q = 0 имеет корни x₁, x₂ и x₃. Выразите через p и q дискриминант этого уравнения

D = (x₁ - x₂)²(x₂ - x₃)²(x₃ - x₁)².

14. Постройте многочлен, корни которого равны квадратам корней многочлена x³ + x² - 2x - 1 = 0.

15. Известно, что x₁, x₂, x₃ — корни уравнения

x³ - 2x² + x + 1 = 0.

Составьте новое уравнение, корнями которого были бы числа y₁ = x₂x₃, y₂ = x₁x₃, y₃ = x₁x₂.

16. Найдите все корни уравнения (z - 1)ⁿ = (z + 1)ⁿ. Чему равна сумма квадратов корней данного уравнения?

Дата добавления: 2015-06-30; просмотров: 306; Нарушение авторских прав

Мы поможем в написании ваших работ!