
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Решение. Первый способ.Пусть утверждение задачи не верно
Первый способ.Пусть утверждение задачи не верно. Числа a, b и c можно сократить на их общий множитель, поэтому будем считать, что НОД(a, b, c) = 1. Пусть одно из чисел не равно ±1, можно считать, что это число a. Пусть p — любой простой делитель числа a. Так как числа взаимно просты в совокупности, p не делит число b или p не делит число c. Рассмотрим второй случай (первый случай аналогичен).
Введем обозначение: k(x) — максимальная степень p в разложении x на простые множители. Можно считать, что k(a) 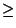 k(b) (мы знаем, что k(c) = 0).
k(b) (мы знаем, что k(c) = 0).
Имеем
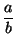 +
+ 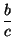 +
+ 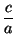 =
= 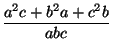 .
.
Число p входит в знаменатель в степени k(a) + k(b). Значит, числитель делится на pk(a) + k(b). Покажем, что это не так. Число p входит в a2c в степени 2k(a) 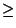 k(a) + k(b), в b2a -- в степени k(a) + 2k(b)
k(a) + k(b), в b2a -- в степени k(a) + 2k(b) 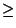 k(a) + k(b), а в c2b — в степени k(b) < k(a) + k(b). Значит, a2c + b2a делится на pk(a) + k(b), а c2b -- не делится на pk(a) + k(b). Поэтому сумма этих чисел не делится на pk(a) + k(b) — противоречие.
k(a) + k(b), а в c2b — в степени k(b) < k(a) + k(b). Значит, a2c + b2a делится на pk(a) + k(b), а c2b -- не делится на pk(a) + k(b). Поэтому сумма этих чисел не делится на pk(a) + k(b) — противоречие.
Второй способ.Введем обозначения: x = 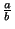 , y =
, y = 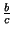 , z =
, z = 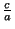 . Тогда xyz = 1 и
. Тогда xyz = 1 и
xy + yz + zx = 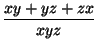 =
= 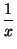 +
+ 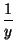 +
+ 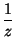 =
= 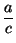 +
+ 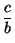 +
+ 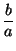
-- целое число. Рассмотрим многочлен
P(t) = t3 - (x + y + z)t2 + (xy + yz + zx)t - xyz.
По доказанному, все коэффициенты этого многочлена целые. Кроме того, коэффициент при старшем члене t3 равен единице. Значит, все рациональные корни этого многочлена — целые (см. комментарий). Согласно обратной теореме Виета, x, y и z — корни этого многочлена. Значит, x, y и z -- целые числа, но xyz = 1, так что x = ±1, y = ±1, z = ±1. Это равносильно тому, что | a| = | b| = | c|.
Комментарий. Докажем использованное утверждение.
Пусть f (x) = a0 + a1x + ... + anxn — многочлен с целыми коэффициентами.
Теорема. Пусть 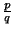 — несократимая дробь, которая является корнем многочлена f (x). Тогда p| a0, q| an.
— несократимая дробь, которая является корнем многочлена f (x). Тогда p| a0, q| an.
Набросок доказательства. Докажем первое утверждение. Условие f[b] 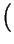
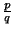
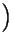 = 0 можно переписать так:
= 0 можно переписать так:
| a0qn + a1pqn - 1 + ... + anpn = 0. | (2) |
Пусть l — простое число. Достаточно доказать, что максимальная степень l, входящая в разложение p на простые множители, не превосходит максимальной степени l, входящей в разложение числа a0 на простые множители. Пусть это не так, т. е. найдется такое x, что p делится на lx, а a0 не делится на lx. Так как дробь 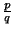 несократима, q не делится на l, поэтому в левой части равенства (*) первый член не делится на lx, а остальные делятся, но это невозможно.
несократима, q не делится на l, поэтому в левой части равенства (*) первый член не делится на lx, а остальные делятся, но это невозможно.
Следствие. Если an = 1, то любой рациональный корень многочлена f (x) является целым.
19. Числа x, y, z удовлетворяют равенству
x + y + z - 2(xy + yz + xz) + 4xyz = 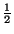 .
.
Докажите, что хотя бы одно из них равно 1/2.
| <== предыдущая страница | | | следующая страница ==> |
| | | Решение. Если левая часть равенства равна нулю, то хотя бы один множитель справа рав |
Дата добавления: 2015-06-30; просмотров: 255; Нарушение авторских прав

Мы поможем в написании ваших работ!