Решение. Если левая часть равенства равна нулю, то хотя бы один множитель справа рав

Заметим, что

x + y + z - 2(xy + yz + xz) + 4xyz - 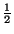= 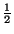(2x - 1)(2y - 1)(2z - 1).

Если левая часть равенства равна нулю, то хотя бы один множитель справа равен нулю. Значит, одно из чисел x, y, z равно 1/2.

Комментарии. 1^o. Как догадаться до разложения на множители? Обозначим этот многочлен через P(x, y, z). Воспользуемся общим утверждением: если многочлен от нескольких переменных тождественно обращается в нуль при x = a, то многочлен делится на x - a. Если x = 1/2, то P(x, y, z) = 0. Значит, P(x, y, z) делится на x - 1/2. Аналогично, P(x, y, z) делится на y - 1/2 и z - 1/2. Поэтому P(x, y, z) равен (x - 1/2)(y - 1/2)(z - 1/2) с точностью до умножения на константу.

2^o. Другой способ: согласно обратной теореме Виета P(x, y, z) = - 4f (1/2), где

f (t) = (t - x)(t - y)(t - z).

20. Целые числа a, b и c таковы, что числа a/b+b/c+c/a и a/c+c/b+b/a тоже целые. Докажите, что |a|=|b|=|c|.

Дата добавления: 2015-06-30; просмотров: 194; Нарушение авторских прав

Мы поможем в написании ваших работ!