
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Задача Коши для обыкновенного дифференциального уравнения первого порядка
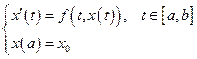
Функция 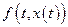 непрерывна. Как было показано, разрешимость данной задачи следует из разрешимости интегрального уравнения:
непрерывна. Как было показано, разрешимость данной задачи следует из разрешимости интегрального уравнения:
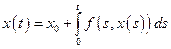 ,
,
которое представим в виде операторного уравнения 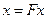 ,
, 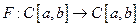 . Всякое непрерывное решение интегрального уравнения является непрерывным решением дифференциального уравнения задачи Коши.
. Всякое непрерывное решение интегрального уравнения является непрерывным решением дифференциального уравнения задачи Коши.
Для доказательства существования неподвижной точки оператора 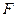 (а это в конечном счете означает, что задача Коши имеет хотя бы одно решение) воспользуемся утверждением следствия. Отметим, что из непрерывности функции двух переменных следует вполне непрерывность оператора
(а это в конечном счете означает, что задача Коши имеет хотя бы одно решение) воспользуемся утверждением следствия. Отметим, что из непрерывности функции двух переменных следует вполне непрерывность оператора 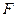 . Доказательство этого факта проводится с применением теоремы Арцела по той же схеме, что и доказательство вполне непрерывности интегрального оператора. Для доказательства существования неподвижной точки остается обеспечить выполнение неравенства в следствии. Для этого предположим, что функция
. Доказательство этого факта проводится с применением теоремы Арцела по той же схеме, что и доказательство вполне непрерывности интегрального оператора. Для доказательства существования неподвижной точки остается обеспечить выполнение неравенства в следствии. Для этого предположим, что функция 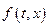 удовлетворяет неравенству:
удовлетворяет неравенству:
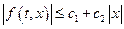 ,
,
Имеем
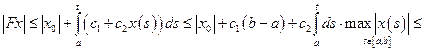
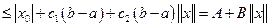 ,
, 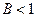
Теорема. Пусть выполнены условия:
-
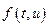 непрерывная функция;
непрерывная функция; - выполняется
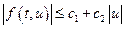 ;
; -
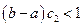 ,
,
следовательно, задача Коши имеет хотя бы одно значение.
Отметим, что в этой теореме, как и в теореме о существовании единственности важное значение имеет произведение длин отрезков на константу 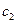 , поэтому в теории дифференциальных уравнений для данной задачи, что бы достичь условия существования или единственности регулируют длину промежутка. Такие утверждения называют локальными в отличии от полученных в данной главе глобальных.
, поэтому в теории дифференциальных уравнений для данной задачи, что бы достичь условия существования или единственности регулируют длину промежутка. Такие утверждения называют локальными в отличии от полученных в данной главе глобальных.
Отметим, что теоремы существования и существования единственности остаются, справедливы и при более слабых ограничениях на функцию двух переменных. Например, необязательно непрерывность 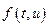 по переменной
по переменной 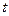 .
.
| <== предыдущая страница | | | следующая страница ==> |
| Теорема Шаудера | | |
Дата добавления: 2015-06-30; просмотров: 298; Нарушение авторских прав

Мы поможем в написании ваших работ!