Теорема Шаудера

Рассмотрим уравнение 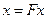с непрерывным оператором .

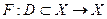Теорема Шаудера. Пусть 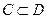- непустое замкнутое выпуклое множество. Если выполнены условия:

1. ;
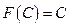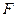2. - вполне непрерывный оператор;

Следовательно, существует хотя бы одна неподвижная точка оператора .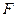

Примем теорему без доказательства.

На практике часто возникает необходимость построения выпуклого множества 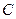. Рассмотрим утверждение (следствие теоремы Шаудера), в котором в качестве 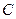выступает замкнутый шар с центром в 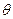и некоторого радиуса .

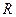Следствие. Пусть вполне непрерывный оператор 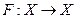удовлетворяет неравенству

, ,

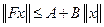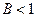следовательно, существует хотя бы одна неподвижная точка.

Неравенство в следствии является ограничением на скорость роста нелинейного оператора 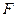. Кроме того, это неравенство является аналогом условия Липшица на бесконечности.

Для доказательства достаточно в силу теоремы Шаудера проверить, что неравенство обеспечивает существование такого замкнутого шара 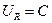, такой что: .

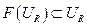Зафиксируем радиус шара 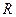и рассмотрим неравенство

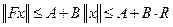, где .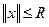

Это неравенство означает, что

,

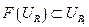где 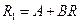. Если 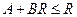, то 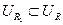, следовательно, для данного радиуса выполняется требуемое вложение .

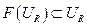Рассмотрим зависимость 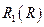. Пусть существует 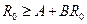, следовательно, для данного радиуса выполняется 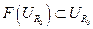, следовательно, выполняются все условия теоремы Шаудера, то есть, вместе с вполне непрерывностью оператор 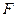отражает непустое выпуклое замкнутое множество в себя 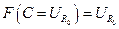, следовательно, существует хотя бы одно решение системы (1), то есть, существует неподвижная точка.

Следствие и теорема гарантируют существование неподвижной точки, но не обеспечивают её единственность.

Дата добавления: 2015-06-30; просмотров: 334; Нарушение авторских прав

Мы поможем в написании ваших работ!