
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Теорема умножения вероятностей (для любых событий, с доказательством)
Вероятность произведения двух событий (совместного появления этих событий) равна произведению вероятности одного из них на условную вероятность другого, вычисленную при условии, что первое событие уже наступило: 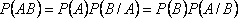
Доказательство. Докажем теорему для случая, когда опыт имеет конечное число несовместных равновероятных исходов.
Пусть:
· событие А появилось в m исходах опыта;
· событие В появилось в k исходах опыта;
· событие АВ появилось в r исходах опыта.
Вероятность события А/В вычислим по классическому определению. Поскольку событие В произошло, то всего возможных в этом случае исходов - k; при этом из этих k возможных исходов благоприятны событию А те исходы, которые составляют событие АВ, т.е. r исходов:
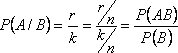 ,
,
Или 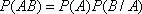 .
.
Следствие 1. Обобщим теорему на случай трех событий:
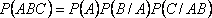
Следствие 2. Обобщим теорему на случай n событий: в случае произведения нескольких зависимых событий вероятность равна произведению одного из них на условные вероятности всех остальных при условии, что вероятность каждого последующего вычисляется в предположении, что все остальные события уже совершились:
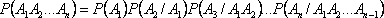 .
.
| <== предыдущая страница | | | следующая страница ==> |
| Числовые ряды, сходимость, сумма ряда, необходимое условие сходимости (с доказательством) | | | Формула Бернулли (с выводом) |
Дата добавления: 2015-06-30; просмотров: 301; Нарушение авторских прав

Мы поможем в написании ваших работ!