Неопределённый интеграл

Интегралы.

Электронный образовательный ресурс

Учебно-методическое пособие к самостоятельному изучению

КУРС ЛЕКЦИЙ

«МАТЕМАТИКА (модуль 2)»

для студентов 1-го курса

отдельных разделов дисциплины «Математика»

(Для студентов всех форм обучения)

Авторы (составители):

к.т.н., доцент О.А. Алейникова

Рассмотрен и рекомендован

для использования в учебном процессе на 2012/2013 – 2017/2018 уч. г. на заседании Кафедры «Математика». Протокол № 1 от 03 09 2012 г.

Шахты 2012

1.1 Первообразная и неопределенный интеграл. Пусть Т – некоторый промежуток на числовой оси, на котором заданы функции f(x) и F(x).

Определение. Функция F(x) называется первообразной функции f(x) на промежутке Т, если .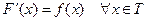

Определение. Пусть функция f задана на промежутке Т. Совокупность всех ее первообразных на этом промежутке называется неопределенным интегралом от функции f и обозначается

.

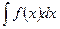Если F(x) – какая-либо первообразная функция f на рассматриваемом промежутке, то

,

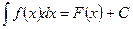где С – произвольная постоянная.

Дата добавления: 2014-02-28; просмотров: 554; Нарушение авторских прав

Мы поможем в написании ваших работ!