Решение. По формуле (1) имеем

df(x) = f ¢(x) dx = .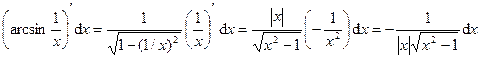

При x =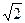получаем df() =. =.

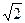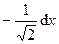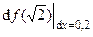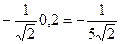5. Найти уравнения касательной и нормали к графику функции 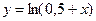при x=0,5.

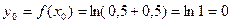Решение. Положим . Тогда . и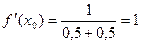. По формуле (5) получаем уравнение касательной 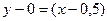или y = x–0,5. По формуле (6) получаем уравнение нормали (y–0)+x–0,5=0 или y=–x+0,5.

6. Исследовать функцию 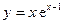на монотонность и экстремумы.

Решение. Область определения – множество всех действительных чисел R.

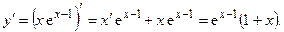Найдем критические точки: 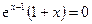Þ x= –1. В интервале (-¥, –1) производная y¢ отрицательна, а в интервале (-1, +¥) – положительна. В силу теоремы 3 исследуемая функция убывает в интервале (-¥, –1) и возрастает в (-1, +¥). По первому достаточному условию экстремума x=1 является точкой минимума. Минимальное значение функции равно .

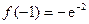7. Исследовать график функции 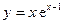на выпуклость, вогнутость и точки перегиба.

Решение. Область определения – множество всех действительных чисел R. Первая производная 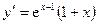(найдена в п. 6). Найдем вторую производную

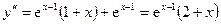. при x=–2. В интервале (-¥, –2) вторая производная y²отрицательна, а в интервале (-2, +¥) – положительна. В силу теоремы 4 график исследуемой функций выпукл в интервале (-¥, –2) и вогнут в (-2, +¥). Так как 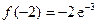, то по достаточному условию точки перегиба (–2, –2e^–3) является точкой перегиба.

8. Найти все асимптоты графика функции .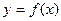

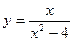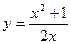1) , 2) , 3)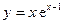

Решение. 1) Функция 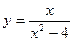не определена при x² – 4 = 0. Следовательно, x = –2 и x=2 являются точками разрыва. Так как односторонние пределы

, , , ,

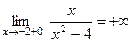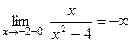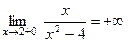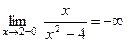то прямые x = –2 и x = 2 являются вертикальными асимптотами.

Поскольку 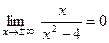, то прямая y=0 является горизонтальной асимптотой при x® ±¥. Наклонных асимптот при x® ±¥ нет, поскольку при этих условиях есть горизонтальная асимптота.

Итак, x = –2 и x = 2 – вертикальные асимптоты, y = 0 – горизонтальная асимптота при x® ±¥.

2) Так как функция 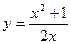не определена при x = 0 и односторонние пределы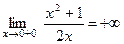, , 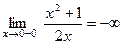то прямая x = 0 является вертикальной асимптотой.

Найдем наклонные асимптоты. По формулам (7) найдем угловой коэффициенты k и b:

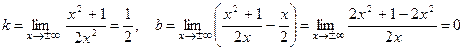. Следовательно, прямая

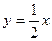является наклонной асимптотой при x® ±¥.

Итак, x = 0 – вертикальная асимптота, 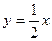– наклонная асимптота при x® ±¥.

3) Функция 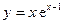определена при любом действительном x,то вертикальных асимптот нет.

Так как 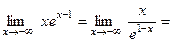(по правилу Лопиталя) =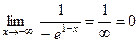, то прямая y = 0 является горизонтальной асимптотой при 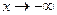. Поскольку 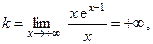то при 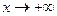нет ни горизонтальных, ни наклонных асимптот.

Итак, y = 0 – горизонтальная асимптота при .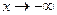

9. Провести полное исследование функции 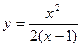и построить ее график.

Решение. Будем следовать схеме исследования функции построения графика из п.13.

1) Область определения функции – множество всех действительных чисел без –1.

2) Функция не является четной, нечетной, периодической.

3) Исследуем функцию на монотонность, экстремумы.

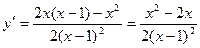. y¢=0 Û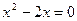Û x=0 или x=2. y¢ не существует в точке x=1, но она не входит в область определения функции. Следовательно, имеются две критические точки x=0 и x=2. Разобьем этими точками область определения на интервалы знакопостоянства производной: (-¥, 0), (0, 1), (1, 2), (2, +¥). Определим знаки производной в этих интервалах: y¢(–1)>0 и y¢(3)>0 Þ в интервалах (-¥, 0) и (2, +¥) производная положительна, y¢(0,1)<0 и y¢(1,1)<0 Þ в интервалах (0, 1) и (1, 2) производная отрицательна (см. рис. 10а). Используя достаточные условия монотонности и экстремума из пунктов 9,10, получим следующие выводы: функция возрастает в интервалах (-¥, 0) и (2, +¥), убывает в (0, 1) и (1, 2), x=0 – точка максимума, x=2 – точка минимума. Значение максимума y(0)=0, значение минимума y(2)=2.

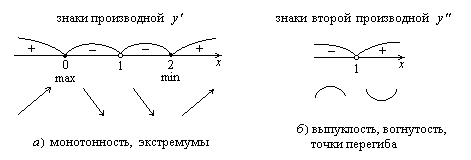Рисунок 10

4) Исследуем функцию на направление выпуклости и точки перегиба.

.

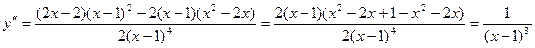y² не обращается в 0, а в точке 1, где y² не существует, функция не определена, поэтому график функции не имеет точки перегиба. Таким образом, имеются два интервала (-¥, 1) и (1, +¥), знакопостоянства второй производной. y²(0)<0 Þ в интервале (-¥, 1) y² отрицательна, y²(2)>0 Þ в интервале (1, +¥) y² положительна (см. рис. 10б). В силу достаточных условий выпуклости и вогнутости графика в интервале (-¥, 1) график выпуклый (вверх), а в интервале (1, +¥) график вогнутый (выпуклый вниз).

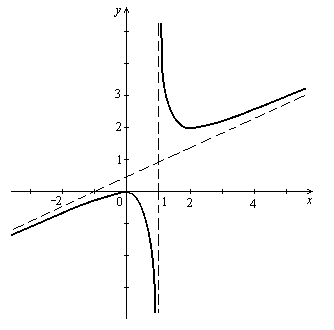Рисунок 11

5) Найдем все асимптоты графика.

Так как, , 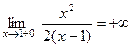то прямая x = 1 – вертикальная асимптота.

Найдем наклонные асимптоты. Для этого по формулам (7) вычислим k и b.

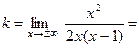(по правилу Лопиталя)= .

.

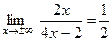Следовательно, прямая 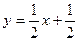– наклонная асимптота при x® ±¥.

6) Так как 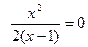Û x = 0, то график пересекает оси системы координат только в ее начале. Найдем дополнительные точки графика: x= –2 Þ y = –2/3 » –0,7; x= 0,8 Þ y = –1,6; x= 1,2 Þ y =3,6; x= 4 Þ y = 8/3 » 2,7.

7) Начертим эскиз графика (рис. 11). Сначала начертим асимптоты x = 1 и 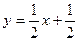(на рисунке они начерчены пунктирной линией). Наносим на чертеж точки (0, 0) и (2, 2), найденные в пункте 3, дополнительные точки (–2; –0,7), (0,8; –1,6), (1,2; 3,6), (4; 2,7), найденные в пункте 6. Проводим через эти точки линию, согласно результатам исследования функции в пунктах 3, 4, 5. Еще раз сравниваем полученный график с результатами исследования и убеждаемся в правильности построения графика.

* проколотой окрестностью точки а называется ее окрестность без а

Дата добавления: 2014-02-28; просмотров: 667; Нарушение авторских прав

Мы поможем в написании ваших работ!