
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Исследование функции и построение ее графика
Сначала приведем определения четной, нечетной, периодической функции.
Функция y=f(x) называется четной (нечетной), если для каждой точки x из области определения она определена в точке -x и f(-x)= f(x) (соответственно f (-x) = f (-x) ).График четной функции симметричен относительно оси Оу, а нечетной функции симметричен относительно начала координат (рис. 7а, 7б).
Функция y = f (x) называется периодической с периодом T ¹ 0, если для любого значения x из области определения она определена в точке x+T и f (x) = f (x+T). Пусть T– наименьший положительный период.График периодической функции с периодом T получается повторением части графика, построенной на отрезке длины T (рис. 7в).
Примерами четных функций являются cosx, chx, |x|, x2. Нечетные функции: sin x, sh x, tg x, ctg x, th x, cth x, x3. Периодические функции: sin x, cosx, (наименьший положительный период 2π), tg x, ctg x, (наименьший положительный период π).
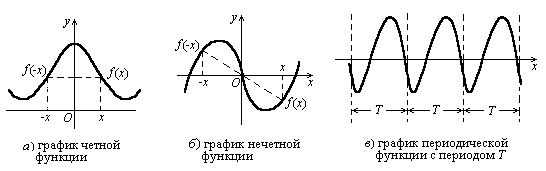 Рисунок 7
Рисунок 7
|
Схема исследования функции. Исследование функции y=f(x) и построение ее графика можно проводить по следующей схеме.
1) Найти область определения.
2) Исследовать на четность, нечетность и периодичность.
3) Исследовать функцию на монотонность, экстремумы.
4) Исследовать функцию на направление выпуклости и точки перегиба.
5) Исследовать функцию на асимптоты.
6) Найти точки пересечения графика функции с осями системы координат.
Схема построения графика функции.График можно строить в следующей последовательности.
1) На оси Ох выделить область определения функции.
2) Начертить все асимптоты, если они есть.
3) Нанести точки графика, где достигаются экстремумы, если они есть.
4) Нанести точки перегиба, если они есть.
5) Нанести точки пересечения графика с осями системы координат, если они есть.
6) При необходимости исследовать поведение функции при x →+ ∞ и -∞.
7) Начертить схематично кривую через нанесенные выше точки, учитывая поведение графика вблизи асимптот и при x →+ ∞ и -∞.
8) Сравнить полученный эскиз с результатами исследования: проверить промежутки монотонности, промежутки выпуклости и вогнутости и т. д.
9) Уточнить эскиз графика. При необходимости найти дополнительные точки графика и начертить график так, чтобы она проходила через эти точки. Если функция четная (нечетная), то график начертить симметрично относительно оси Оу (соответственно начала координат). Если функция периодическая с наименьшим периодом T > 0, то построить часть графика на одном интервале длины T и повторить ее через период.
Пример.17) Провести полное исследование функции 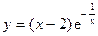 и построить ее график.
и построить ее график.
Решение. Функцию исследуем согласно схеме.
1) Область определения – множество всех действительных чисел, таких, что x ¹ 0. Точка x = 0 является точкой разрыва функции.
2) Функция не является четной, нечетной, периодической.
3) Найдем первую производную:
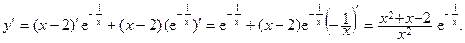
Решим уравнение y¢= 0: 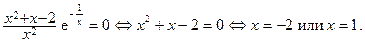 Производная не существует в точке x = 0, но в ней функция не определена, поэтому она не является критической. Таким образом, критическими являются точки x = -2 и x = 1. Разобьем им область определения на интервалы и нейдем в них знаки производной (рис. 8а). Так как
Производная не существует в точке x = 0, но в ней функция не определена, поэтому она не является критической. Таким образом, критическими являются точки x = -2 и x = 1. Разобьем им область определения на интервалы и нейдем в них знаки производной (рис. 8а). Так как 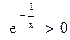 и
и 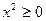 , то знак производной совпадает со знаком квадратного трехчлена
, то знак производной совпадает со знаком квадратного трехчлена  . Его значение в интервалах (-∞, -2) и (1, +∞) положительно, а в интервалах (-2, 0) и (0, 1) отрицательно. Таким образом, функция возрастает в интервалах (-∞, -2) и (1, +∞), убывает в интервалах (-2, 0) и (0, 1), x = -2 – точка максимума, максимальное значение равно
. Его значение в интервалах (-∞, -2) и (1, +∞) положительно, а в интервалах (-2, 0) и (0, 1) отрицательно. Таким образом, функция возрастает в интервалах (-∞, -2) и (1, +∞), убывает в интервалах (-2, 0) и (0, 1), x = -2 – точка максимума, максимальное значение равно 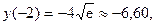 x = 1 – точка минимума, минимальное значение равно
x = 1 – точка минимума, минимальное значение равно 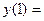
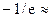
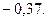
4) Найдем вторую производную:
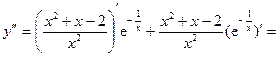
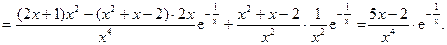
Вторая производная существует во всех точках области определения функции, значит, точка перегиба может быть только при таких значениях х, что у′′ = 0. Решив уравнение 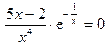 , получим х = 2/5 = 0,4. Этой точкой разобьем область определения функции на интервалы (рис. 8б). Чтобы определить знаки второй производной в этих интервалах, возьмем в каждой из них по одной точке (например, -1, 0.1, 1) и найдем знаки у² в этих точках: у²(-1) < 0, у²(0.1) < 0, у²(1) > 0. Следовательно, у²< 0 в интервалах (-∞,0) и (0, 0.4), у²> 0 в интервале (0.4,+∞) (рис. 8б).
, получим х = 2/5 = 0,4. Этой точкой разобьем область определения функции на интервалы (рис. 8б). Чтобы определить знаки второй производной в этих интервалах, возьмем в каждой из них по одной точке (например, -1, 0.1, 1) и найдем знаки у² в этих точках: у²(-1) < 0, у²(0.1) < 0, у²(1) > 0. Следовательно, у²< 0 в интервалах (-∞,0) и (0, 0.4), у²> 0 в интервале (0.4,+∞) (рис. 8б).
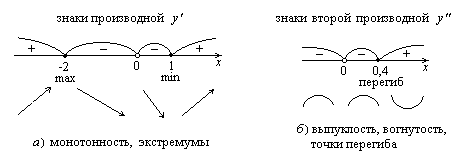 Рисунок 8
Рисунок 8
|
Таким образом, функция выпукла вверх в интервалах (-∞,0) и (0, 0.4), выпукла вниз в интервале (0.4,+∞), x = 0.4 является абсциссой точки перегиба, 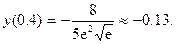
5) Вертикальная асимптота может быть в точке разрыва x = 0. Найдем односторонние пределы функции в этой точке.
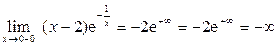 ,
, 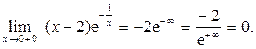
Следовательно, прямая x = 0 является вертикальной асимптотой при x → 0 слева, при этом график функции бесконечно приближается к асимптоте, уходя в -∞ (вниз).
Горизонтальных асимптот нет, так как 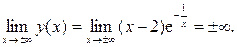
Найдем наклонные асимптоты по формулам (7).
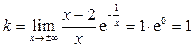 .
.
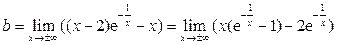
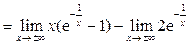 .
.
По правилу Лопиталя
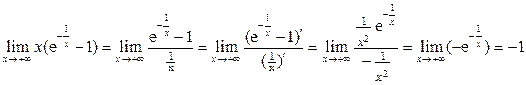 .
.

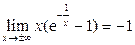 .
.
Таким образом, b = -3 и прямая у = х – 3 является наклонной асимптотой при x →±∞.
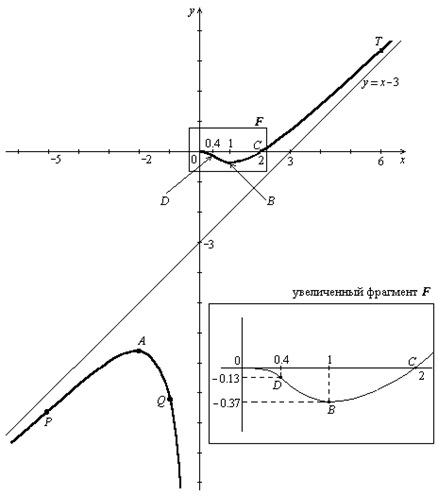 Рисунок 9
Рисунок 9
|
6) Так как в точке x = 0 функция не определена и
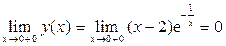 ,
,  ,
,
то график функции “подходит” справа к началу координат.
Чтобы найти точки пересечения графика функции с осью Ох , решим уравнение
у(х) = 0:  Значит, график пересекает ось Ох при x = 2.
Значит, график пересекает ось Ох при x = 2.
Построим график функции по результатам исследования, следуя схеме построения графика, описанной выше (см. рис. 9).
1) Область определения не содержит точку 0, значит, график не пересекает ось Оу.
2) Начертим асимптоту у = х – 3, вертикальная асимптота совпадает с осью Оу.
3) Наносим точки А (-2, ≈-6.60) и В (1, ≈-0.37), где функция достигает соответственно максимума и минимума.
4) Наносим точку перегиба D (0.4, ≈-0.13).
5) Отметим начало координат, к которой “подходит” график слева, и точку С (2, 0) пересечения графика с осью Ох.
6) Так как 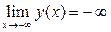 и
и 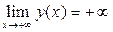 , то при x →-∞ график “уходит” вниз, а при x →+∞ - вверх.
, то при x →-∞ график “уходит” вниз, а при x →+∞ - вверх.
7) Поскольку прямая у = х – 3 асимптота при x →-∞, то проводим кривую от А влево и вниз так, чтобы она приближалась к прямой у = х – 3. При этом выпуклость направим вверх. Затем от точки А проводим кривую вправо и вниз, приближая ее к асимптоте х = 0. При этом выпуклость по-прежнему направим вверх. Соединим начало координат с точкой перегиба D “убывающей” кривой выпуклостью вверх. Соединим точку D с точкой В “убывающей” кривой выпуклостью вниз. Соединим точку В с точкой С “возрастающей” кривой выпуклостью вниз. Наконец, проводим от точки С кривую вправо и вверх выпуклостью вниз так, чтобы она приближалась к асимптоте у = х – 3.
8) Для контроля сравниваем полученный эскиз графика с результатами исследования функции. Интервалы монотонности и экстремумы, интервалы выпуклости и вогнутости, точки перегиба эскиза графика совпадают с результатами исследования. Поведение графика на эскизе вблизи асимптот и при больших по модулю значениях переменной х согласуется с результатами исследования.
9) Для уточнения графика найдем несколько точек вблизи асимптот.
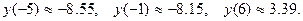 Соответствующие точки на рис. 9 обозначены буквами P, Q, T . На рис. 9 приведен увеличенный фрагмент F графика, где более точно изображено поведение графика около точки перегиба D.
Соответствующие точки на рис. 9 обозначены буквами P, Q, T . На рис. 9 приведен увеличенный фрагмент F графика, где более точно изображено поведение графика около точки перегиба D.
Задачи с решениями
1.Найти производные следующих функций.
1) 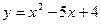 ; 2)
; 2) 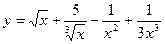 ;
;
3) 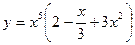 ; 4)
; 4) 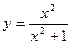 ;
;
5) 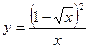 ; 6)
; 6) 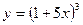 ;
;
7) 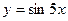 ; 8)
; 8) 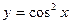 ;
;
9) 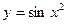 ; 10)
; 10) 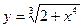 ;
;
11) 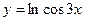 ; 12)
; 12) 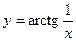 .
.
Решение. 1)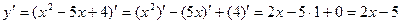 (по правилам дифференцирования (1), (2) и формулам 1 и 4 таблицы ).
(по правилам дифференцирования (1), (2) и формулам 1 и 4 таблицы ).
2) Преобразуем данную функцию к виду 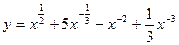 .
.
Применяя правила (1), (2) и формулу 4 таблицы, получим
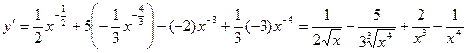 .
.
3) Сначала раскроем скобки, затем продифференцируем:
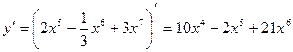 .
.
4) Пользуясь правилом (4) дифференцирования дроби, получим
 .
.
5) Вначале раскроем скобки и произведем деление числителя на знаменатель почленно, далее продифференцируем:

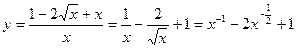 ;
; 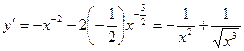 .
.
6) Полагая 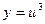 , где
, где 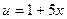 , и применяя формулу (2) для дифференцирования сложной функции, имеем:
, и применяя формулу (2) для дифференцирования сложной функции, имеем:
 ;
; 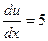 ;
; 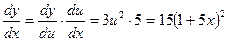 .
.
Легко проверить правильность этого результата: возведя в куб и дифференцируя полученный многочлен, приходим к тому же ответу.
7) Полагая 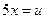 и пользуясь формулой 10 таблицы и правилом дифференцирования сложной функции (2), найдем
и пользуясь формулой 10 таблицы и правилом дифференцирования сложной функции (2), найдем
 .
.
8) Полагая  и применяя формулу (2) и формулы 4 и 11 таблицы, получим
и применяя формулу (2) и формулы 4 и 11 таблицы, получим
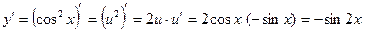 .
.
9) При 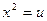 по формуле (2) и формулам 10 и 4 таблицы найдем
по формуле (2) и формулам 10 и 4 таблицы найдем
 .
.
10) Полагаем 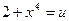 . Пользуясь формулой 4 таблицы, имеем
. Пользуясь формулой 4 таблицы, имеем
 .
.
Дифференцирование этой сложной функции можно записать иначе:
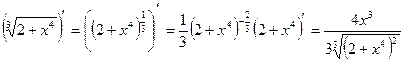 .
.
Второй способ записи без особого обозначения промежуточного аргумента значительно проще. Этому способу записи и следует научиться при дифференцировании сложных функций.
11) Согласно формулам 8, 11 таблицы и формуле (2) имеем

 .
.
12) По формуле (2) и формулам 16 и 4 таблицы имеем
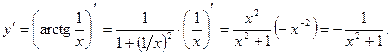
2. Найти производные высших порядков функции 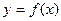 и их значения.
и их значения.
1) 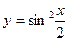 , найти
, найти 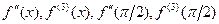 .
.
2) 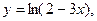 .найти
.найти 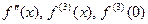 .
.
Решение. 1) 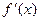 =
=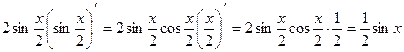 .
.
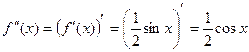 .
. 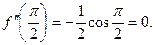
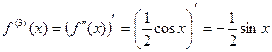 .
. 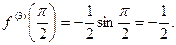
2)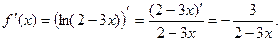
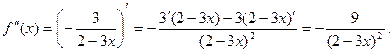
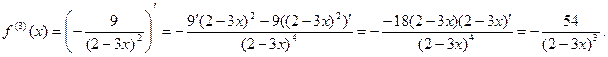
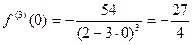 .
.
3.Для функций, заданных параметрически, найти указанные производные.
1) 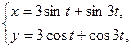 найти
найти 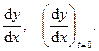
2) 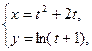 найти
найти 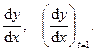
Решение. 1) Находим производные от 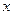 и от
и от 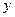 по параметру
по параметру 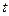
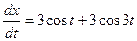 ,
, 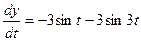 .
.
Искомую производную от 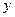 по
по 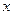 находим по формуле (3):
находим по формуле (3):
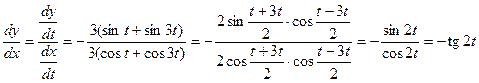 .
.
При 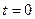 получим
получим 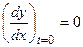 .
.
2) Вычисляем производные функций 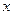 и
и 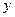 по параметру
по параметру 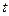 :
:
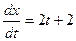 ,
, 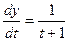
и искомую производную функции 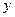 по
по 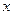 по формуле (3):
по формуле (3):
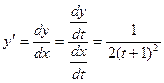 .
.
Далее, при  имеем
имеем  .
.
4. Найти дифференциал df(x) функции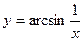 . Найти df(
. Найти df(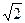 ) и
) и 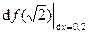 .
.
| <== предыдущая страница | | | следующая страница ==> |
| Так как то горизонтальных асимптот нет | | | Решение. По формуле (1) имеем |
Дата добавления: 2014-02-28; просмотров: 2099; Нарушение авторских прав

Мы поможем в написании ваших работ!