
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Примеры. Из простых высказываний с помощью некоторого числа логических операций можно построит
Логические операции
Примеры.
- Число 100 делится на 5.
- Число 3 больше числа 5.
- Луна больше Земли.
- Сегодня светит солнце.
- Вечером мы пойдем в кино.
Из простых высказываний с помощью некоторого числа логических операций можно построить сложные высказывания.
- Число 100 делится на 5 и число 100 делится на 10.
- Неверно, что 3 больше 5.
- Сегодня мы пойдем в кино или мы пойдем в театр.
При изучении логики высказываний не обращают внимание на содержание простых высказываний, а интересуются только их истинностью или ложностью.
Сложные высказывания, получаемые из простых, будут также истинными или ложными. Их истинность или ложность будет зависеть от истинности образующих их простых высказываний.
Для изучения логических операций введем следующую систему обозначений:
· простые высказывания будем обозначать буквами a, b, c, …, x, y ,z;
· значения истинности будем обозначать 1 – истинно, 0 – ложно.
Действия логических операций будем представлять в виде таблиц истинности.
1. Отрицание или инверсия (Ø – НЕ)
Пример.
а: 7 делится на 5 без остатка.
Øа: Неверно, что 7 делится на 5 без остатка.
| а | Øа |
Эта таблица и принимается в качестве определения операции отрицания.
2. Конъюнкция ( Ù,&, ·, логическое И )
Действие операции определяется следующим образом: сложное высказывание а&b истинно только в том случае, когда оба высказывания (а и b) имеют значение истинно.
| а | b | а&b |
а. 6 делится на 3 без остатка (1);
b. 10 больше 5 (1);
с. 7 делится на 3 без остатка (0);
d. 3 больше 7 (0);
a&b=1
a&c=0
c&d=0
3. Дизъюнкция (Ú,+,логическое ИЛИ)
Действие операции определяется следующим образом: сложное высказывание аÚв ложно только в том случае, когда оба высказывания (а и в) ложны.
| a | b | aÚb |
Примеры.
аÚb=1
aÚc=1
cÚd=0
4. Импликация (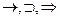 ) “если а, то b”
) “если а, то b”
Действие операции определяется следующим образом: сложное высказывание а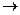 b ложно только в том случае, когда а истинно, а b – ложно.
b ложно только в том случае, когда а истинно, а b – ложно.
| a | b | a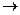 b b
|
А называется антецедентом, а b – консеквентом.
5. Эквивалентность (~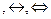 )
)
Действие операции определяется следующим образом: сложное высказывание а~b истинно, если а истинно и b истинно, или если а ложно и b ложно.
| a | b | a~b |
Эквивалентность примерно соответствует употреблению выражения «тогда и только тогда».
6. сумма по модулю два 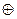
| a | b | a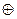 b b
|
7. Штрих Шеффера ( ê, обратная конъюнкция И – НЕ)
| a | b | a ê b |
8. Стрелка Пирса (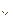 , обратная дизъюнкция ИЛИ – НЕ )
, обратная дизъюнкция ИЛИ – НЕ )
| a | b | a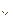 b b
|
Используя эти логические операции можно строить сколь угодно сложные высказывания.
Приоритет выполнения операций:
⌐ & Ú 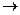 ~
~ 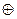 ê
ê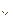
Пример: Сложное высказывание: «Если вы не пропускаете занятия и успешно занимаетесь, то Вы сдадите экзамен хорошо» можно записать следующим образом. Обозначим:
П – пропускаете занятия;
Y – успешно занимаетесь;
Х – сдадите экзамен хорошо,
тогда все высказывание запишется:
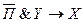
Значение истинности всего выражения будет зависеть от истинности переменных обозначающих простые высказывания.
| <== предыдущая страница | | | следующая страница ==> |
| Понятие высказывания | | |
Дата добавления: 2014-02-28; просмотров: 524; Нарушение авторских прав

Мы поможем в написании ваших работ!