Ряд Маклорена

Предположим, что функция f x), n раз непрерывно дифференцируемая в окрестности точки х = 0, может быть представлена в виде суммы степенного ряда или разложена в степенной ряд:

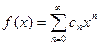
Тогда этот ряд имеет вид:

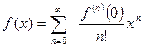
Этот ряд называется рядом Маклорена.

Можно доказать, что разложение в ряд Маклорена единственно.

Теперь рассмотрим разложение в ряд Маклорена некоторых функций.

1.

Область сходимости ряда .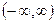

2.

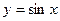
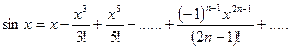
Область сходимости ряда ).

3.

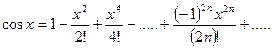
Область сходимости ряда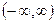

4.

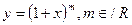
Интервал сходимости (-1; 1), на концах интервала при х = 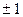сходимость ряда зависит от конкретных значений m.

Этот ряд называется биномиальным. Если то биномиальный ряд представляет формулу бинома Ньютона, так как при n = m + 1 n-й член ряда и все последующие равны нулю и вместо бесконечного разложения получается конечная сумма.

5.

Рассмотрим геометрический ряд

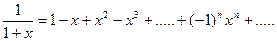со знаменателем q = -x, который сходится при 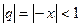к функции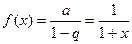

Интегрируем этот ряд почленно в интервале (0; х), где :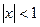

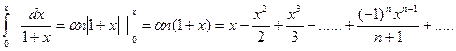
Область сходимости ряда (-1; 1].

Вопросы для самоконтроля знаний:

1. Как разложить функцию в ряд Тейлора и Маклорена?

Дата добавления: 2014-02-28; просмотров: 713; Нарушение авторских прав

Мы поможем в написании ваших работ!