Свойства степенных рядов

Пусть функция 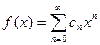, т.е. является суммой степенного ряда. На любом отрезке 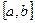, целиком принадлежащем интервалу сходимости (-R, R), функция f (x) является непрерывной и степенный ряд можно почленно интегрировать на этом отрезке:

Кроме того, в интервале сходимости степенной ряд можно почлено дифференцировать:

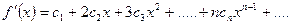
При этом после интегрирования или дифференцирования полученные ряды имеют тот же радиус сходимости R.

Более того, два степенных ряда можно почленно складывать и умножать по правилу сложения и умножения многочленов . При этом полученный новый ряд будет иметь промежуток сходимости, совпадающий с общей частью промежутков сходимости исходных рядов.

Дата добавления: 2014-02-28; просмотров: 586; Нарушение авторских прав

Мы поможем в написании ваших работ!