
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Степенные ряды
Лекция 13
План лекции:
1. Область сходимости степенного ряда
2. Теорема Абеля.
3. Ряды Тейлора и Маклорена
Ряды, членами которых являются степенные функции, называются степенными рядами. Они имеют вид:
c0 + c1x + c2x2 + …..+ cnxn + ….= 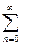 cnxn (1)
cnxn (1)
Область сходимости степенного ряда.
Совокупность тех знаний х, при которых степенной ряд(1) сходится, называется областью сходимости степенного ряда.
Пример. Найти область сходимости ряда.
1 + х + х2 +…..+хn +…..
Решение. Данный ряд можно рассматривать как геометрический ряд со знаменателем q = x, который сходится при  . Поэтому областью сходимости является интервал (-1; 1).
. Поэтому областью сходимости является интервал (-1; 1).
Структура области сходимости устанавливается с помощью теоремы Абеля.
Теорема Абеля. 1.) Если степенной ряд сходится при х0  , то он абсолютно сходится и при всех
, то он абсолютно сходится и при всех  .
.
2.) Если степенный ряд расходится при х = х1, то он расходится и при всех 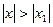 .
.
Из теоремы Абеля следует, что  :
: - ряд сходится,
- ряд сходится, 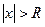 - ряд расходится.
- ряд расходится.
Число R называется радиусом сходимости, а интервал (-R, R) – интервалом сходимости.
На концах интервала сходимости при х = -R и х = R ряд может как сходиться, так и расходиться.
Найдем выражение для радиуса сходимости ряда (1) через его коэффициенты. Рассмотрим 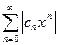 из абсолютных величин членов ряда (1), в котором все коэффициенты сn, начиная с некоторого номера n, отличны от нуля. По признаку Даламбера этот ряд сходится, если
из абсолютных величин членов ряда (1), в котором все коэффициенты сn, начиная с некоторого номера n, отличны от нуля. По признаку Даламбера этот ряд сходится, если


Если этот предел существует, то он и является радиусом сходимости ряда (1):

Пример. Найти радиус сходимости степенного ряда:
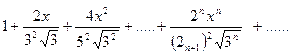
Решение. Найдем радиус сходимости ряда по формуле :
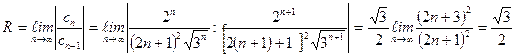
Интервал сходимости ряда -  .
.
Теперь выясним поведение ряда при 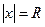 . При
. При  ряд принимает вид
ряд принимает вид
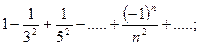 он сходится по признаку Лейбница. При
он сходится по признаку Лейбница. При 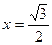 получаем ряд
получаем ряд  . Это обобщенный гармонический ряд при
. Это обобщенный гармонический ряд при  , которого все члены с четными номерами равны нулю.
, которого все члены с четными номерами равны нулю.  , поэтому ряд сходится. Таким образом, область сходимости имеет вид:
, поэтому ряд сходится. Таким образом, область сходимости имеет вид: 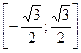
| <== предыдущая страница | | | следующая страница ==> |
| Ряды с произвольными членами | | | Свойства степенных рядов |
Дата добавления: 2014-02-28; просмотров: 901; Нарушение авторских прав

Мы поможем в написании ваших работ!