Ряды с произвольными членами

Ряд, в котором члены попеременно положительны и отрицательны, т.е. называется знакочередующимся.

Теорема (признак Лейбница). Если в знакочередующемся ряде члены ряда убывают по абсолютной величине и 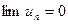, то ряд сходится, а его сумма не превосходит первого члена, т.е..

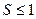Пример. Исследовать сходимость ряда

Решение. Ряд знакочередующийся, его члены убывают по абсолютной величине; предел общего члена , по признаку Лейбница ряд сходится.

Следствие. Погрешность при приближенном вычислении суммы сходящегося знакочередующегося ряда, удовлетворяющего условиям теоремы Лейбница, по абсолютной величине не превышает абсолютной величины первого отброшенного члена.

Пример. Какое число членов ряда 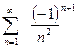, надо взять, чтобы вычислить его с точностью до 0,001?

Решение. По условию . Учитывая следствие, запишем более сильное неравенство: 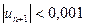или 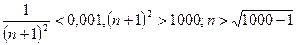, или n>30,6, т.е необходимо взять не менее 31 члена ряда.

Ряд, в котором любой его член u_n может быть как положительным, так и отрицательным, называется знакопеременным.

Теорема (достаточный признак сходимости знакопеременного ряда). Если ряд 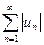, составленный из абсолютных величин членов ряда 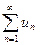, сходится, то сходится и данный ряд.

Замечание. Обратное утверждение неверно: ряд 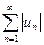может расходиться, а ряд 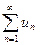сходиться. Например, ряд сходится по признаку Лейбница, а ряд из абсолютных величин его членов является гармоническим и расходится.

Ряд называется абсолютно сходящимся, если сходится как сам ряд, так и ряд, составленный из абсолютных величин его членов.

Ряд называется условно сходящимся, если сам ряд сходится, а ряд, составленный из абсолютных величин его членов, расходится.

Например, ряд 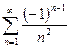- абсолютно сходящийся, а ряд - условно сходящийся.

Различие между абсолютно сходящимися и условно сходящимися рядами: первые сходятся за счет главным образом быстрого убывания их членов, а вторые в результате того, что положительные и отрицательные члены ряда уничтожают друг друга.

Вопросы для самоконтроля знаний.

1. Понятие ряда и его сходимость

2. Знакопеременные и знакочередующиеся ряды.

Дата добавления: 2014-02-28; просмотров: 757; Нарушение авторских прав

Мы поможем в написании ваших работ!