Ряды с положительными членами

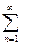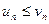Теорема ( признак сравнения) .Пусть даны два ряда с положительными членами u_n и, причем для любого n Тогда:

а) если сходится второй ряд, то сходится и первый;

б) если расходится первый ряд, то расходится и второй.

Замечание. Условие 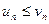не обязательно должно выполняться для первых членов ряда и только для членов с одинаковыми номерами. Достаточно,

чтобы оно выполнялось, начиная с некоторого номера n = k или чтобы имело место неравенство , .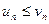

Существуют «эталонные ряды», которые часто используются для сравнения:

1) геометрический ряд 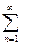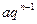сходится при и расходится при ;

2) гармонический ряд расходится;

3) обобщенный гармонический ряд 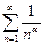сходится при и расходится при .

Пример. Исследовать сходимость ряда .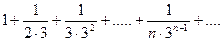

Решение. Сравним данный ряд со сходящимся геометрическим рядом 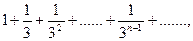для которого а = 1, q = 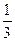. Члены данного ряда, начиная со второго, меньше членов сходящегося геометрического ряда: 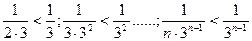, следовательно на основании признака сравнения ряд сходится.

Теорема ( предельный признак сравнения). Есл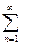и и - ряды с положительными членами и существует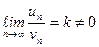, то ряды одновременно сходятся либо расходятся.

Пример. Исследовать сходимость ряда .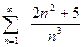

Решение. Сравним данный ряд с гармоническим

:

Данный ряд, как и гармонический, расходится.

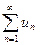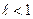Теорема (признак Даламбера). Пусть для ряда с положительными членами.Тогда, если, то ряд сходится, если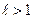, то ряд расходится, при 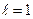вопрос о сходимости ряда остается открытым.

Пример. Исследовать сходимость ряда :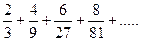

Решение. Общий член ряда имеет вид 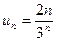, тогда u_n+1 = 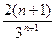.Применим признак Даламбера:

По признаку Даламбера ряд сходится.

Теорема (интегральный признак сходимости). Пусть 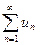- ряд с положительными невозрастающими членами; пусть f (x) – непрерывная невозрастающая функция, определенная при 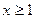, и f (1)=u₁,

f (2)= u₂…..,f (n)=u_n….

Тогда для сходимости ряда необходимо и достаточно, чтобы сходился несобственный интеграл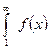

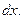
Пример. Исследовать сходимость обобщенного гармонического ряда

Решение. Пусть f (x) = . Функция f (x) при х >0 положительная и невозрастающая (даже убывающая). Поэтому сходимость ряда равносильна сходимости несобственного интеграла 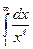. Имеем

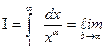
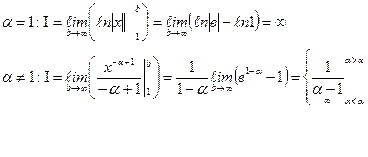
Ряд сходится при и расходится при

Пример. Исследовать по интегральному признаку сходимость ряда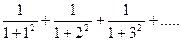

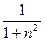Решение. Пусть f (x) = . Общий член ряда u_n = совпадает с f (x) при натуральных n; функция f (x) положительная и невозрастающая (убывающая). Поэтому можно применить интегральный признак сходимости:

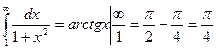
Следовательно, ряд сходится.

Дата добавления: 2014-02-28; просмотров: 857; Нарушение авторских прав

Мы поможем в написании ваших работ!