Необходимый признак сходимости

Установить сходимость ряда путем определения S_n и вычисление 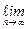S_n не всегда возможно из – за трудностей при нахождении S_n. Проще сделать это с помощью признаков сходимости.

Теорема (необходимый признак сходимости). Если ряд сходится, то 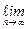u_n =0

Следствие. Если 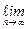u_n0, то ряд расходится.

Рассмотренный признак не является достаточным. Если 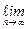u_n = 0. то из этого не следует, что ряд сходится.

В качестве примера рассмотрим гармонический ряд Здесь

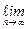u_n = 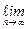= 0. Однако гармонический ряд расходится. Запишем суммы первых

2 n и n членов ряда:

S_2n= 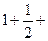(2n слагаемых);

S_n = (n слагаемых );

S_2n – S_2n =

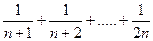
Заменим в последнем выражении каждое слагаемое меньшим, равным :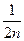

S_2n – S_2n >или S_2n – S_n >

Предположим, что гармонический ряд сходится, тогда 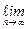S_n = 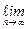S_2n = S.

Перейдем к пределу в предыдущем неравенстве, получим:

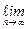(S_2n – S_n) = S – S = 0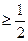

Получили противоречие с предположением о сходимости ряда, следовательно, ряд расходится.

Дата добавления: 2014-02-28; просмотров: 470; Нарушение авторских прав

Мы поможем в написании ваших работ!