
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Вопрос 2. Выполнение группировки по количественному признаку
В основание группировки могут быть положены как количественные, так и качественные признаки. После определения основания группировки, следует решить вопрос о количестве групп, на которые надо разбить изучаемую совокупность.
Число групп зависит от задач исследования и вида признака, положенного в основание группировки, численности совокупности, степени вариации признака.
При построении группировки по качественному признаку групп, как правило, будет столько, сколько имеется градаций, видов, состояний у этого признака. Например, в случае проведения группировки населения по полу можно образовать только две группы: мужчины и женщины.
Если группировка проводится по количественному признаку, то необходимо обратить особое внимание на число единиц исследуемого объекта . На количество выделяемых групп существенное влияние оказывает степень вариации группировочного признака: чем она больше, тем больше следует образовывать групп.
Для определения количества групп необходимо придерживаться двух важных условий построения группировок:
1) Выделенные группы должны отличаться качественной однородностью;
2) Количество единиц в каждой группе должно быть достаточно большим.
Оптимальное количество групп с равными интерваламиможно определить по формулеамериканского ученого Стерджесса :

где N - число единиц совокупности.
Другой способ определения числа групп основан на применении показателя среднего квадратического отклонения ( ). Если величина интервала равна 0,5
). Если величина интервала равна 0,5 , то совокупность разбивается на 12 групп, а когда величина интервала равна
, то совокупность разбивается на 12 групп, а когда величина интервала равна 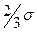 и
и  , то совокупность делится соответственно на 9 и 6 групп.
, то совокупность делится соответственно на 9 и 6 групп.
Если совокупность разбивается на 12 групп, то интервалы групп строятся следующим образом:
от 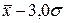 до
до 
от  до
до 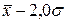
от 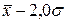 до
до 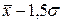
от 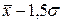 до
до 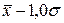
от 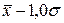 до
до 
от 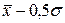 до
до 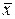
от 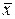 до
до 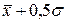
от 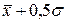 до
до 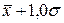
от 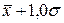 до
до 
от  до
до 
от  до
до 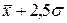
от 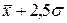 до
до 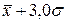
где  - среднее значение признака по совокупности, которое определяется по формуле
- среднее значение признака по совокупности, которое определяется по формуле 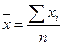 ,
,
 - среднее квадратическое отклонение, согласно формуле :
- среднее квадратическое отклонение, согласно формуле :
 .
.
где 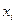 - i-e значение варьирующего признака;
- i-e значение варьирующего признака;
Когда число групп равно 6, получаются следующие интервалы групп:
от 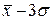 до
до 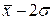
от 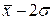 до
до 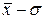
от 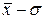 до
до 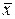
от 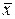 до
до 
от  до
до 
от  до
до 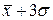
После определения количества групп следует определить интервалы группировки.
Интервал– это количественное значение , отделяющее одну единицу (группу)от другой, т.е. интервал очерчивает количественные границы групп.
Каждый интервал имеет:
1.Нижняя границаинтервала - это наименьшее значение признака в интервале;
2.Верхняя граница -наибольшее значение признака в нем.
3.Величина интервала(ее еще часто называют интервальной разностью) представляет собой разность между верхней и нижней границами интервала.
Интервалы группировки в зависимости от их величины бывают:
1)равные;
2) неравные:
а) прогрессивно возрастающие,
б) прогрессивно убывающие,
в) произвольные
г) специализированные.
Если вариация признака проявляется в сравнительно узких границах и распределение носит более или менее равномерный характер, то строят группировку с равными интервалами.
Величина равного интервала определяется по следующей формуле:

где R =  - размах вариации;
- размах вариации;
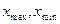 - максимальное и минимальное значения признака в совокупности.
- максимальное и минимальное значения признака в совокупности.
Полученную по формуле величину округляют..
Существуют следующие правила определения величины интервала:
1. Если величина интервала, представляет собой величину, имеющую один знак до запятой (например, 0,66; 1,372; 5,8), то полученные значения целесообразно округлить до десятых и их использовать в качестве шага интервала.
2.Когда рассчитанная величина интервала имеет две значащие цифры до запятой и несколько знаков после запятой, то это значение надо округлить до целого числа.
3. В случае, когда рассчитанная величина интервала представляет собой трехзначное, четырехзначное и так далее число, эту величину необходимо округлить до ближайшего числа, кратного 100 или 50
Интервалы также могут быть:.
1. Открытые- это те интервалы, у которых указана только одна граница: верхняя - у первого, нижняя - у последнего. Ширина открытого интервала принимается равной ширине смежного с ним интервала.
2.Закрытыминазываются интервалы, у которых обозначены обе границы.
Неравные интервалы могут быть прогрессивно возрастающие или убывающие в арифметической или геометрической прогрессии. Величина интервалов, изменяющихся в арифметической прогрессии, определяется следующим образом:
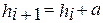
в геометрической прогрессии:

где а - константа - число, которое будет положительным при прогрессивно возрастающих интервалах и отрицательным - при прогрессивно убывающих интервалах;
q - константа - положительное число, которое при прогрессивно возрастающих интервалах будет больше 1, а при прогрессивно убывающих меньше 1.
3.Специализированныминазываются интервалы, применяющиеся для выделения из совокупности одних и тех же типов по одному и тому же признаку для явлений, находящихся в различных условиях.
| <== предыдущая страница | | | следующая страница ==> |
| Вопрос 1. Задачи и виды группировок | | | Вопрос 3. Ряды распределения |
Дата добавления: 2014-03-11; просмотров: 992; Нарушение авторских прав

Мы поможем в написании ваших работ!