
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Этапы работы с теоремой Упражнения, реализующие их
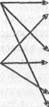
|
| Мотивация изучения теоремы |
Упражнения на измерение величин,на оперирование моделями фигур
Упражнения с практическим содержанием
| Ознакомление с теоремой |
| Усвоение содержания теоремы |
Упражнения на применение ранее изученных теорем и понятий

|
Упражнения на выделение условия и заключения теоремы
| Запоминание формулировки теоремы |
Упражнения на распознавание ситуаций, удовлетворяющих теореме
Упражнения на выполнение чертежей, моделирующих условие теоремы
| Ознакомление со способом доказательства Доказательство теоремы |
Упражнения на ознакомление с методом доказательства теоремы
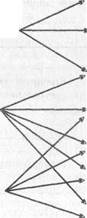
Упражнения, моделирующие способ доказательства
Упражнения на выделение в доказательстве недостающих утверждений и их обоснований
| Применение теоремы |
Упражнения на систематизацию теорем
Упражнения на составление «родословной» теоремы
| Установление связей теоремы с теоремами, изученными ранее |
Упражнения на составление плана доказательства теоремы
Упражнения на составление алгоритмов
2-й способ. Можно организовать самостоятельную работу по специальным карточкам, задание предлагается на готовом чертеже. Карточка содержит и указания, число которых зависит от возможностей учащихся.
Еще раз подчеркнем важность заключительного этапа работы с упражнением. Основная его цель заключается в выявлении зависимости между углом ABC и дугой АС, на которую он опирается, и метода ее установления, суть которого в следующем:
зависимость между /_АВС и ^АС устанавливается посредством введения LAOC, отношения которого с углом ABC и дугой АС известны.
Итак, выполнение упражнения позволило открыть зависимость между вписанным углом и дугой, на которую он опирается, и способ ее обоснования в том случае, когда сторона угла содержит диаметр окружности. Теперь можно сформулировать теорему, выполнить рисунок, записать «Дано», «Требуется доказать» и коллективно наметить способ доказательства. Оформление доказательства учащиеся могут выполнить самостоятельно. Доказательство теоремы во втором и третьем случаях может быть рассмотрено самостоятельно в классе либо дома, при этом, естественно, учитель показывает, как эти случаи сводятся к первому случаю.
Работа с доказательством теоремы в основном случае может быть организована и по-другому. Сильные учащиеся могут разобрать доказательство сами, некоторым же учащимся может быть оказана помощь в виде упражнений на специальных карточках. Приведем один из возможных вариантов такой карточки.
Основанием для ее составления является доказательство теоремы о вписанном угле, оформленное в виде данной таблицы.
| Утверждения | Обоснования |
| 2. 3. ЛАОВ — равнобедренный 4. LABO=LBAO 5. LAOC=LABO+LBAO 7. | Внешний угол равнобедренного треугольника АВО Утверждения 6 и 1 |
Количество пропусков определяется способностями учащихся. Такие карточки могут быть подготовлены учителем и даны учащимся при домашнем (или классном) разборе двух других случаев.
При обсуждении работы по карточкам следует прибегать к развертыванию того или иного логического шага. Например:
Шаг 3. В приведенной карточке ученик, продолжая строчку 3, запишет: ОА= ОС. Развертывание этого силлогизма предполагает указать большую, малую посылку и вывод.
Выполнение заданий на развертывание логических шагов может осуществляться как письменно, так и устно.
Заметим, что акцентирование внимания школьников на дедуктивных выводах может осуществляться при выполнении упражнений на распознавание объектов, принадлежащих понятию, на выведение следствий из факта принадлежности объекта понятию, т. е. в процессе формирования понятия вписанного угла.
Закрепив теорему о вписанном угле на ряде простых упражнений на нахождение по данным рисунка либо величины вписанного угла, либо дуги окружности, переходим к решению более сложной задачи. Пусть это будет задача 658 («Геометрия, 7—9» авторов Л. С. Атана-сяна и др.):
Через точку А к данной окружности проведены касательная АВ (В — точка касания) и секущая AD, проходящая через центр О (D — точка на окружности, О лежит между А и D). Найдите /LBAD и ^ADB, если -fiZ)=110°20' (рис. 1).
Данную задачу можно решать разными способами. Рассмотрим один из них.
Z.BOD= 110°20'. В равнобедренном треугольнике BOD <LOBD = = ^ODB=34°50'. /.BAO = /-BOD-AABO=U0°20'-90°=20°20'.
Полезно обратить внимание учащихся на угол DBK (К — точка луча АВ, не лежащая между А и В). Он равен 55°10'. Этот угол хотя и не является вписанным, но имеет с ним много общего: его вершина принадлежит окружности, одна сторона пересекает окружность, а другая является касательной к ней. Из решения задачи следует, что, этот угол, т. е. угол, образованный касательной и хордой окружности, проведенной из точки касания, измеряется половиной дуги, заключенной внутри его.
Обратим внимание на угол BAD. Замечаем, что он равен полуразности дуг BD и BE. Сформулируем замеченное утверждение: угол, вершина которого лежит вне круга, а стороны образуют касательная, проведенная через вершину, и секущая, проходящая через центр круга, измеряется полуразностью дуг, заключенных между его сторонами. Обобщая это утверждение, мы приходим к гипотезе о том, что угол, вершина которого лежит вне круга, а стороны его пересекают круг, измеряется полуразностью дуг, заключенных между его сторонами.
Итак, фиксируем первое сформулированное утверждение: угол, образованный касательной и хордой, измеряется половиной дуги, заключенной внутри его. Использование теоремы о том, что касательная к окружности перпендикулярна радиусу, проведенному в точку касания, позволяет легко обосновать частный случай утверждения: угол, образованный касательной и диаметром, измеряется половиной дуги, заключенной внутри его. Последнее усиливает мысль о справедливости утверждения, к доказательству которого следует перейти. Отметим, что в учебнике А. В. Погорелова оно значится как задача 59 (§ 11).
Теперь можно перейти к обоснованию второго сформулированного утверждения. Однако опять-таки попробуем убедиться в его справедливости. Этому поможет, например, задача 661 (учебник Л. С. Атанасяна и др.):
Найдите острый угол, образованный двумя секущими, проведенными из точки, лежащей вне окружности, если дуги, заключенные между секущими, равны 140° и 52°.
Решение данной задачи моделирует доказательство утверждения в общем случае.
Возникает проблема выяснения связи угла, образованного двумя пересекающимися хордами окружности, с дугами, заключенными внутри сторон. Эта проблема содержится в задаче 662.
Хорды АВ и CD окружности пересекаются в точке Е. Найдите угол ВЕС, если wAD=54°, ^5C=70°.
Выполнение этого упражнения позволит ученику самостоятельно решить указанную проблему. Более того, оно открывает ученику содержание теоремы о пересечении хорд окружности. Действительно, в процессе решения задачи легко установить подобие треугольников АСЕ и BED, откуда и будет следовать равенство, фиксируемое в указанной теореме. (Ниже рассмотрен иной подход к ознакомлению школьников с этой теоремой.)
 В развитие темы «Вписанные углы» можно предусмотреть задачи на оценку способов доказательства, опровержение готовых доказательств и т. д.
В развитие темы «Вписанные углы» можно предусмотреть задачи на оценку способов доказательства, опровержение готовых доказательств и т. д.
 Пример:
Пример:
Задача 663: Отрезок АС — диаметр окружности, АВ — хорда, МА — касательная, угол МАВ острый. Докажите, что /_МАВ = /LACB.
Авторы учебника предполагают, по-видимому, решение, не основанное на утверждении о том, что угол, образованный касательной и хордой, измеряется половиной дуги, заключенной внутри его (оно рассматривается в следующей задаче): /-МАВ = 90°- /LBAC- /-ACB. В следующей задаче 664 требуется доказать, что угол МАВ измеряется половиной дуги АВ, расположенной внутри угла МАВ, где AM — касательная к окружности, АВ — хорда этой окружности.
Возникает вопрос: можно ли решение предыдущей задачи считать доказательством данного утверждения? (Полнота доказательства утверждения предполагает рассмотрение случая, когда угол, образованный касательной и хордой, является тупым.)
И еще один важный аспект в контексте обучения доказательству — формирование эвристик. Равенство углов, связанных с многоугольником, иногда удается доказать, введя вписанные углы, т. е. описать около многоугольника или его части окружность. В качестве примера рассмотрим задачу 732.
В прямоугольном треугольнике ABC из точки М стороны АС проведен перпендикуляр МН к гипотенузе АВ. Докажите, что углы МНС и МВС равны.
В четырехугольнике НМСВ противоположные углы И и С — прямые, поэтому около него можно описать окружность. В новой конструкции углы МНС и МВС являются вписанными, опирающимися на дугу МС.
3.2. Теорема о пересечении хорд окружности. Актуализация опорных знаний и умений может быть осуществлена посредством серии упражнений:
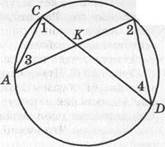 а) выделите на рисунке 2 вписанные углы;
а) выделите на рисунке 2 вписанные углы;
| В |
б) определите, каково соотношение
между ними;
в) сделайте вывод об отношении
между треугольниками АКС и BKD;
г) запишите отношение между сторонами этих треугольников.
Можно выполнить упражнения на переход от соотношения вида АК-ВК= = CK-KD к соотношению вида АК: СК= KD■ ВК, которое используется в доказательстве теоремы.
| Рис. 2 |
Указанная последовательность упражнений позволяет не только актуализировать опорные знания, но и служит приемом проверки изученного на предыдущем уроке материала. Организация выполнения упражнений может быть осуществлена разными способами:
а) Учитель заранее выполняет рисунок на доске, предъявляет учащим
ся вопросы, и осуществляется коллективное выполнение упражнения.
б) Ученикам выдается карточка с рисунком, на доске вывешивает
ся плакат с вопросами (формулировки вопросов могут быть зафик
сированы на доске и с помощью кодоскопа). Учащиеся самостоятель
но выполняют упражнения, учитель при этом консультирует учащихся
и координирует их действия.
Проследим действия учащихся:
а) вписанные углы: /L\, Z.2, Z3, /LA\
| б) в) |
-/-2 (опираются на Z.3=Z4 (опираются на
AAKC^ABKD (Z.1 = ZL2, Ll- /.4); АК _СК _ АС
KD KB BD' Предлагаем учащимся записать первое равенство отношений
AK-KD = CK-KB, содержащееся в пропорции г), в виде равенства произведений АК-КВ = KD-CK. Читаем полученное равенство: если две хорды окружности пересекаются, то произведение отрезков одной хорды равно произведению отрезков другой хорды. Затем сообщается теорема о пересечении хорд, учащиеся в тетрадях выполняют рисунок, учитель может выполнить его на доске (этот рисунок служит и средством контроля правильности выполнения рисунка учащимися), записывается (в тетрадях и на доске) факт, подлежащий доказательству.
Обратим внимание читателя на то, что открытие теоремы учащимися было сделано посредством выполнения цепочки упражнений, актуализирующих опорные знания и умения, адекватные рассматриваемой теореме. Учащиеся были подведены сразу к общей формулировке закономерности. В данной ситуации этот путь является самым оптимальным, потому что открыть теорему посредством измерений, построений малоестественно.
Работа с доказательством теоремы может быть осуществлена по-разному. Она может вестись в контексте как восходящего анализа, так и нисходящего. Рассмотрим эти приемы:
а) Коллективный поиск способа доказательства с последующей самостоятельной работой.
Учитель ведет примерно следующую беседу с учащимися.
Учитель. Итак, нам нужно доказать равенство двух произведений. Каким образом можно преобразовать это равенство? (Предыдущие упражнения помогут проявлению нужного действия: преобразовать равенство произведений в равенство отношений АК- KD = CK:KB.)
Учитель. Что нужно знать для доказательства полученного равенства?
Ученик. Подобие треугольников АКС и BDK.
Учитель. Что можно утверждать об указанных треугольниках?
Ученик. £.\=/L2, Z.3 = /l4 (либо LAKC =/_BKD).
Затем осуществляется самостоятельная работа с учебником. Учитель акцентирует внимание учащихся на основных положениях доказательства. (Почему /A —/L21 Откуда следует подобие треугольников АКС и BKD1 Что следует из подобия этих треугольников?)
б) Коллективный поиск способа доказательства с последующим
использованием карточек.
Первая часть приема осуществляется так же, как и в предыдущем случае. Вторая часть приема реализуется с помощью карточек. Вот одна из них.
| Утверждения | Обоснования | ||
| 2. 3. | |||
| Углы вертикальные | |||
| AAKC^ABKD | |||
| 4. | AK:DK=CK:BK | ||
| 5, | Утверждение 4 | ||
Естественно, некоторые ученики могут разобраться в доказательстве без карточек, другие нуждаются в более тщательном пояснении (карточки для них будут содержать незначительное число пропусков).
в) Самостоятельная работа с учебником. Этот прием может быть
реализован следующим образом. Учитель предлагает учащимся прочитать абзац доказательства и ответить на вопросы. Чтение первого абзаца сопровождается вопросами: о каких фигурах идет речь в прочитанном абзаце? Могут ли эти хорды располагаться не так, как на рисунке учебника? (Они могут быть перпендикулярными, одна из хорд либо обе могут быть диаметрами окружности.)
Усвоение второго абзаца осуществляется посредством ответов на вопросы: почему 1Л**1Л1 Почему Z3 = zl4? Почему AAKC<*ABKD7
Откуда следует равенство 7>F = 7rF' Почему утверждаем, что
AKBK=CKDK? Ш ВК
г) Коллективный поиск способа доказательства теоремы и коллективное доказательство.
Этот прием отличается от рассмотренных выше тем, что доказательство осуществляется всеми учащимися под руководством учителя. При этом запись некоторых шагов доказательства на доске учителем может осуществляться после соответствующей записи учащимися в тетрадях.
Работу с доказательством можно вести и в контексте нисходящего анализа. Этот вид соотносится с приемом опровержения утверждения: из утверждения выводится следствие, противоречащее заведомо истинному предложению. Если же окажется, что к такому следствию не придем, тогда усиливается уверенность в справедливости доказываемого утверждения и находится отправное положение в доказательстве теоремы.
Итак, пусть
AKKB = KD CK.
(1)
т
Из верности равенства (1) следует верность равенства
| (2) |
АК_СК DK ВК'
Из равенства (2) и того, что углы АКС и DKB вертикальные, следует подобие треугольников АКС и DKB.
| <== предыдущая страница | | | следующая страница ==> |
| Подробно о возрасте от 14 до 19 лет | | | Характеристика работы Л.Н. Толстого «Закон насилия и закон любви» |
Дата добавления: 2015-06-30; просмотров: 447; Нарушение авторских прав

Мы поможем в написании ваших работ!