В декартовой системе координат каждой точке плоскости соответствует пара действительных чисел и, наоборот, каждой паре чисел соответствует определенная точка на плоскости

В аналитической геометрии всякую линию рассматривают как геометрическое место точек, удовлетворяющих определенному свойству, которое записывается в виде уравнения.

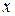· Уравнением линии на плоскости называется уравнение с двумя переменными и 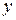, которому удовлетворяют координаты любой точки, лежащей на линии, и не удовлетворяют координаты ни одной точки, не лежащей на ней. Входящие в это уравнение координаты 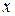и 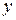произвольной точки линии называются текущими координатами.

Пример. Лежит ли точка на линии, заданной уравнением ?

Подставим координаты точки в уравнение линии: . Так как , то точка не лежит на линии.

В аналитической геометрии решаются две задачи:

1. Зная геометрические свойства объекта, написать его уравнение.

2. Зная уравнение геометрического объекта, изучить его форму и свойства.

Дата добавления: 2015-06-30; просмотров: 267; Нарушение авторских прав

Мы поможем в написании ваших работ!