Прямая на плоскости и ее уравнения

Изучение геометрических свойств линий начнем с простейшей линии – прямой.

Теорема. Каждая прямая на плоскости 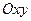определяется линейным уравнением первой степени с двумя неизвестными. Обратно: каждое линейное уравнение первого порядка с двумя неизвестными определяет некоторую прямую на плоскости.

Пример 4.1. Постройте прямую, заданную уравнением .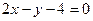

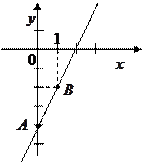
Для построения прямой достаточно знать координаты двух её произвольных точек. Полагая в уравнении прямой, например, 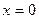, получим 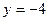. Имеем точку 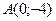. Полагая 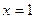, получим 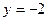. Отсюда вторая точка 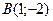. Результаты вычислений можно занести в таблицу:

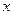
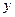
	-4	-2

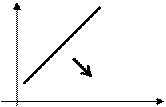
Осталось построить точки и провести через них прямую (см. рисунок).

1. Уравнение прямой, проходящей через данную точку с заданным нормальным вектором:

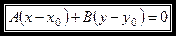, (1)

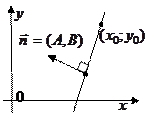где 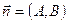— нормальный вектор прямой, 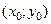— координаты данной точки.

Вектор 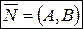, координаты которого равны коэффициентам при переменных 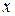и 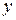в общем уравнении прямой, называется нормальным вектором прямой (перпендикулярным данной прямой).

2. Общим уравнением прямой на плоскости называется уравнение первой степени относительно 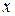и : ,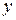

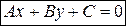где 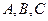— постоянные коэффициенты, причём 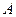и 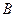одновременно не обращаются в нуль .

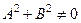Частные случаи этого уравнения:

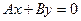
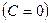— прямая проходит через начало координат;

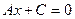
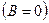— прямая параллельна оси ;

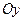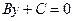
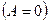— прямая параллельна оси ;

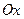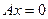
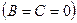— прямая совпадает с осью ;

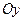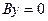
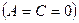— прямая совпадает с осью .

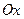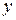
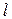
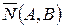
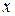
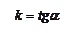
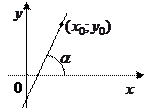3. Уравнение прямой, проходящей через данную точку и с заданным угловым коэффициентом:

,

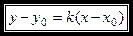где 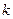— угловой коэффициент прямой, 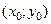— координаты данной точки.

 

4. Уравнение прямой с угловым коэффициентом имеет вид:

,

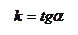
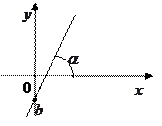
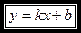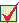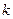где — угловой коэффициент прямой (т.е. тангенс угла 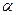, который прямая образует с положительным направлением оси 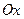), 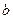— ордината точки пересечения прямой с осью .

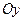Под углом 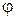наклона прямой к оси ОХ будем понимать тот наименьший угол, на который надо повернуть ось ОХ против часовой стрелки, чтобы она совпала с прямой.

 

 

Если 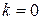, то прямая параллельна оси абсцисс, ее уравнение .

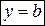Если 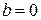, то прямая проходит через начало координат, ее уравнение .

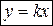Для прямой, параллельной оси ординат, уравнение имеет вид .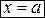

 

5. Уравнение прямой, проходящей через две данные точки 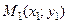и , где 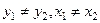имеет вид:

 

.

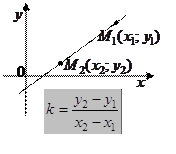
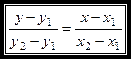В случае 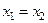уравнение прямой примет вид 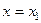. В случае 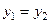уравнение прямой: .

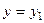Пример. Напишите уравнение прямой, проходящей через точку 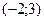параллельно прямой .

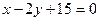Из уравнения прямой 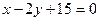выпишем координаты нормального вектора: 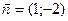. Так как прямые параллельны, то в качестве нормального вектора для искомой прямой примем этот же вектор. Имеем, 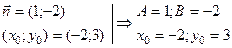. Воспользуемся формулой (1):

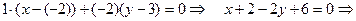
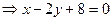— уравнение искомой прямой.

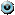Ответ: 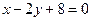— уравнение искомой прямой.

 

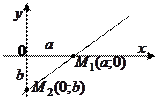6. Уравнение прямой в отрезках:

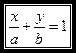, (3)

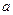где и 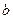— длины отрезков (с учётом знаков), отсекаемых прямой на осях 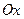и 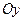соответственно.

 

Таким образом, один и тот же геометрический объект (прямая) может быть описан или задан несколькими видами уравнений.

Дата добавления: 2015-06-30; просмотров: 313; Нарушение авторских прав

Мы поможем в написании ваших работ!