Неравенство Чебышева

Получим вначале некоторые оценки для распределений случайных величин.

Лемма. Если неотрицательная случайная величина имеет конечное математическое ожидание 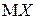, то для любого 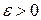справедливо неравенство:

.

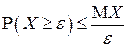▲ Докажем лемму для непрерывной случайной величины (для дискретной случайной величины доказать самостоятельно). По определению математического ожидания непрерывной случайной величины

,

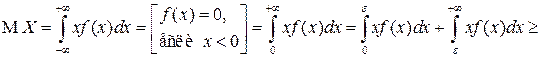
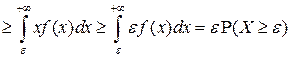откуда и следует утверждение леммы ■.

Следствие (неравенство Чебышева). Если случайная величина имеет конечную дисперсию 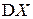, то для любого 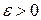справедливы следующие неравенства:

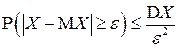; (4.15)

.

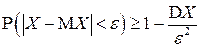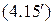
▲ В соответствии с предыдущей леммой

,

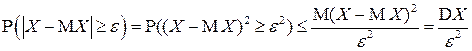что доказывает неравенство (4.15). Неравенство 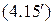следует из (4.15) путем перехода к противоположному событию ■.

Неравенство Чебышева имеет большое теоретическое и практическое значение. Оно дает простую оценку для вероятности отклонения случайной величины с произвольным законом распределения от ее математического ожидания. Причем, если о случайной величине, кроме ее математического ожидания и дисперсии ничего неизвестно, то эту оценку улучшить нельзя (существует пример случайной величины, для которой в (4.15) достигается равенство). Если же есть дополнительная информация о случайной величине (например, известен ее закон распределения), то оценки (4.15) и 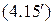могут быть существенно улучшены.

Пример. Пусть случайная величина имеет нормальный закон распределения: 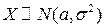. Тогда:

- на основании неравенства Чебышева

;

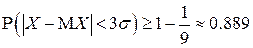- в соответствии с «правилом »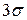

,

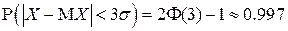где 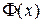- функция Лапласа.

Дата добавления: 2015-06-30; просмотров: 348; Нарушение авторских прав

Мы поможем в написании ваших работ!