Виды сходимости последовательностей случайных величин и связь между ними

Как и в математическом анализе, в теории вероятностей имеют дело с различными видами сходимости последовательностей случайных величин. Основными среди них являются: сходимость по вероятности, сходимость почти наверное и сходимость в среднем порядка 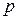(в среднем квадратическом).

Пусть на вероятностном пространстве 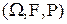заданы последовательность случайных величин 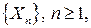и величина (случайная или нет).

Определение. Говорят, что последовательность случайных величин 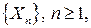сходится по вероятности к величине , если для любого

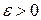
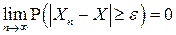
или, что эквивалентно,

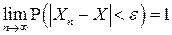
Краткое обозначение сходимости по вероятност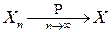и: или 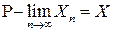. В математическом анализе этот вид сходимости называется сходимостью по мере.

Определение. Говорят, что последовательность случайных величин 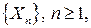сходится почти наверное к величине (почти всюду, с вероятностью 1), если

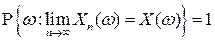
или, что эквивалентно,

.

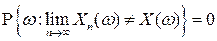Краткое обозначение сходимости почти наверное: .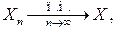

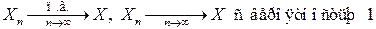Другими словам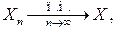и, если 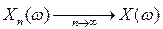для всех 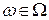, за исключением, быть может, 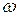из множества 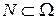, имеющего нулевую вероятность: .

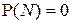Смысл этой сходимости в математическом анализе - почти поточечная сходимость последовательности функций.

Определение. Говорят, что последовательность случайных величин 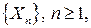сходится к величине в среднем порядка 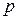( ), если

.

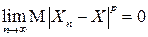Краткое обозначение сходимости в среднем порядка :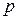
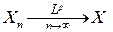
(в данном определении предполагается, что все случайные величины обладают конечными моментами до порядка 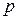включительно).

В математическом анализе этот вид сходимости называется сходимостью в смысле 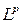(в гильбертовом пространстве порядка ).

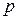Сходимость в среднем порядка 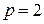называют сходимостью в среднем квадратическом и используют запись: 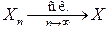или 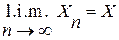(limit in the mean). В дальнейшем мы будем иметь дело в основном с этим видом сходимости в среднем.

Смысл введенных видов сходимостей последовательностей случайных величин: понятие предела определено только для числовой последовательности, поэтому случайность под знаком предела должна быть ликвидирована. Это делается в приведенных определениях либо с помощью вероятности, либо с помощью математического ожидания со своим понятием близости между 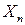и .

Лемма (связь между видами сходимостей).

а) Если последовательность случайных величин 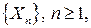сходится к величине почти наверное, то она сходится к этой величине и по вероятности:

.

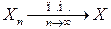
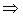
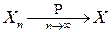б) Если последовательность случайных величин 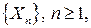сходится к величине в среднем порядка 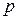( ), то она сходится к этой величине и по вероятности:

.

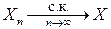
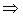
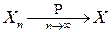▲ а) Если 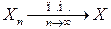, то по определению сходимости почти наверное на множестве 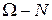( 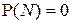), начиная с некоторого 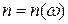, при любом 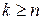и для любого 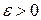справедливо неравенство: 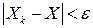. Другими словами,

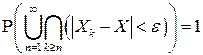
или, переходя к противоположному событию:

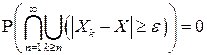. (4.16)

Покажем, что равенство (4.16) эквивалентно тому, что

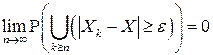. (4.17)

Действительно, поскольку при любом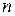

,

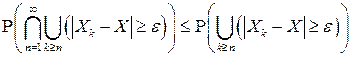то, переходя в обеих частях данного неравенства к пределу при 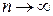, получаем, что из (4.17) следует (4.16), так как вероятность не может быть отрицательной (лемма о двух милиционерах).

Для доказательства того, что из (4.16) следует (4.17), рассмотрим события 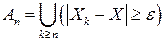. Поскольку 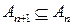и 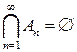в соответствии с (4.16), то 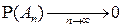в силу аксиомы непрерывности вероятности Р4).

Для окончательного доказательства утверждения а) леммы достаточно заметить, что для любого 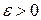в соответствии с (4.17)

.

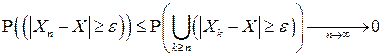Поэтому 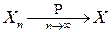(в соответствии с леммой о двух милиционерах).

б) Зафиксируем 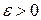. Тогда в силу неравенства Чебышева для любого

.

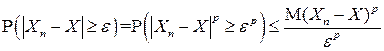Поэтому, если 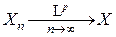, то 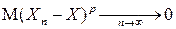и, следовательно, для любого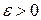 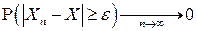(снова в соответствии с леммой о двух милиционерах) ■.

Замечание. Из леммы следует, что сходимость по вероятности является слабейшей из всех введенных трех видов сходимостей последовательностей случайных величин. Обратные импликации в утверждениях а) и б) леммы, вообще говоря, неверны (соответствующие примеры можно найти в учебнике А.А. Боровкова «Теория вероятностей»).

Дата добавления: 2015-06-30; просмотров: 880; Нарушение авторских прав

Мы поможем в написании ваших работ!