Законы больших чисел

Типичным примером применения на практике законов больших чисел является следующая задача об измерениях в условиях помех.

Предположим, что производится измерение некоторой физической величины 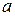. При этом в действительности результат измерения есть значение случайной величины 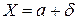, где 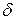- погрешность измерения, которую естественно считать случайной величиной с 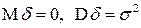. Для повышения точности измерения величины 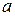на практике всегда поступают следующим образом. Измерения производят как можно в большем количестве и в одинаковых условиях, стараясь обеспечить независимость измерений друг от друга. Получают при этом результаты 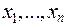(значения случайной величины ). В качестве приближенного значения величины 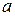принимают среднее арифметическое результатов измерений:

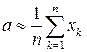. (4.18)

Законы больших чисел позволяют:

- указать точный смысл приближенного равенства (4.18);

- ответить на вопрос о точности приближенного равенства (4.18);

- указать условия, при которых утверждения типа приближенного равенства (4.18) справедливы.

Определение. Говорят, что последовательность случайных величин 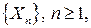имеющих конечные математические ожидания 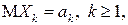подчиняется закону больших чисел, если для любого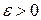

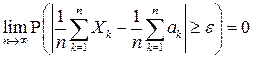(4.19),

или, более кратко,

.

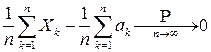Важно выделить частный случай, когда все случайные величины в последовательности 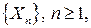имеют одинаковые математические ожидания 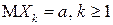. Тогда утверждение закона больших чисел (4.19) принимает вид:

,

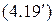
то есть

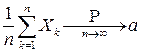
(в частности, утверждение закона больших чисел, имеет вид 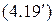для одинаково распределенных случайных величин).

Рассмотрим несколько вариантов законов больших чисел, причем начнем с наиболее общего из них.

Теорема 1 (Маркова) (Закон больших чисел для зависимых, разнораспределенных случайных величин).

Пусть 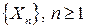- последовательность случайных величин, имеющих конечные математические ожидания 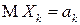и дисперсии 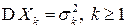, для которых выполняется условие:

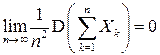. (условие Маркова)

Тогда эта последовательность случайных величин подчиняется закону больших чисел, то есть выполняется соотношение (4.19).

▲ Обозначим 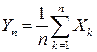. Тогда по свойствам математического ожидания и дисперсии имеем:

.

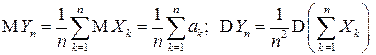В силу неравенства Чебышева (4.15)

.

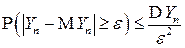Но по условию Маркова 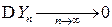. Поэтому, переходя в последнем соотношении к пределу при 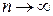, получаем, что для любого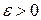 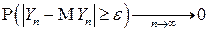, то есть 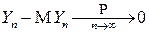(лемма о двух милиционерах) ■.

Теорема 2 (Чебышева) (Закон больших чисел для некоррелированных, разнораспределенных случайных величин).

Пусть 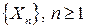- последовательность попарно некоррелированных (в частности, попарно независимых) случайных величин, дисперсии которых равномерно ограничены, то есть

.

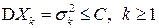Тогда эта последовательность случайных величин подчиняется закону больших чисел, то есть выполняется соотношение (4.19).

▲ Снова обозначим 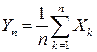. Тогда 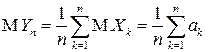, а в силу аддитивности дисперсии для попарно некоррелированных случайных величин имеем:

.

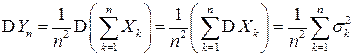В соответствии с неравенством Чебышева (4.15)

.

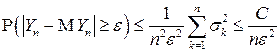Переходя далее к пределу при 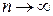, получаем, что для любого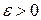 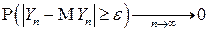, то есть ■.

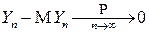Замечание 1. Теорема Чебышева является фактически следствием теоремы Маркова, поскольку из равномерной ограниченности дисперсий случайных величин следует выполнение условия Маркова (что и было продемонстрировано при доказательстве теоремы).

Замечание 2. Утверждение теоремы Чебышева остается справедливым и при более слабом, чем равномерная ограниченность дисперсий, условии:

.

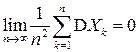Теорема 3 (Закон больших чисел для независимых, одинаково распределенных случайных величин).

Если случайные величины в последовательности 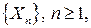являются независимыми, одинаково распределенными и имеют конечные математические ожидания 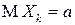и дисперсии 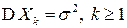, то эта последовательность случайных величин подчиняется закону больших чисел, то есть

.

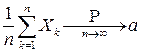▲ Обозначим по-прежнему 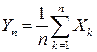. Тогда

.

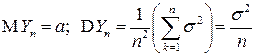В соответствии с неравенством Чебышева (4.15) имеем:

.

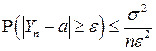Переходя в последнем соотношении к пределу при 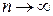, получаем, что для любого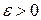 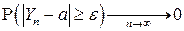, то есть ■.

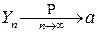Замечание 1. Теорема 3 является очевидным следствием теоремы Чебышева и ее можно было бы не доказывать. Доказательство приведено здесь только для того, чтобы утверждению теоремы придать самостоятельность.

Вернемся теперь к задаче об измерениях в условиях помех.

Проведение 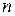независимых наблюдений над случайной величиной 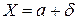, где 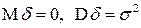, эквивалентно проведению одного наблюдения над 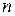независимыми, распределенными также как случайными величинами 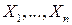. При этом 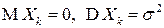для любого 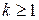. В силу Теоремы 3 такая последовательность случайных величин 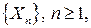подчиняется закону больших чисел, то есть

.

Таким образом, среднее арифметическое результатов измерений при больших 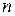мало отличается от измеряемой величины 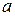с вероятностью, близкой к 1. Это и есть точный смысл приближенного равенства (4.18).

Точность приближенного равенства (4.18) характеризуется величиной дисперсии среднего арифметического измерений

,

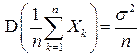которая оказывается в 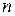раз выше, чем точность одного измерения, равная 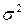. Этот факт и объясняет требование к проведению на практике как можно большего числа измерений в условиях, обеспечивающих их независимость друг от друга.

Теорема 4 (Бернулли).

Относительная частота 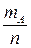появления события 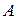в 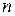независимых испытаниях, проводимых по схеме Бернулли, сходится по вероятности при 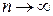к вероятности 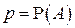наступления события 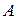в одном испытании, то есть для любого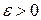

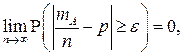
или, кратко

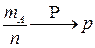при .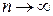

▲ Обозначим 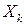- число появлений события А в 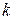-ом испытании. Случайная величина 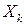принимает два значения 1 и 0 с вероятностями:

.

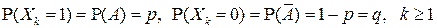Все случайные величины 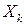, являются независимыми и одинаково распределенными, причем для любого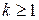

.

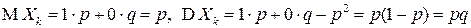В силу Теоремы 3 такая последовательность случайных величин 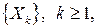подчиняется закону больших чисел, то есть

.

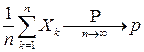Осталось заметить, что 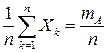, и поэтому ■.

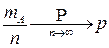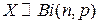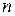Замечание. Пусть . Поскольку случайная величина - число успехов в независимых испытаниях по схеме Бернулли, то ее можно представить в виде:

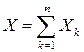, (4.20)

где 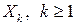- случайные величины из доказательства теоремы Бернулли (их называют еще бернуллиевскими). Из представления (4.20), свойств математического ожидания и дисперсии и того, что 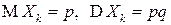, имеем:

.

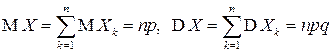Это есть более простой способ нахождения числовых характеристик биномиальной случайной величины, чем просто по определению (как это делалось ранее).

Теорема Бернулли является обоснованием статистического определения вероятности, в соответствии с которым за неизвестную вероятность 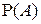события 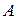принимается его известная относительная частота 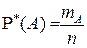появления в 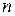независимых испытаниях. Теорема Бернулли утверждает, что действительно вероятность неравенства 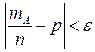для сколь угодно малого 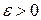может быть при достаточно большом числе испытаний 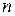сделана как угодно близкой к 1.

Физическая суть законов больших чисел состоит в том, что различные по алгебраическим знакам случайные отклонения независимых (или слабо зависимых) случайных величин 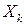, 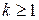от их общего среднего значения при большом 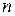в массе своей взаимно погашаются. Поэтому, хотя сами величины 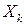, 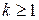и случайны, но их среднее 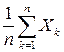при достаточно большом 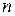практически уже неслучайно.

Из законов больших чисел также следует, что путем усреднения наблюдаемых значений любой случайной величины можно достаточно точно определить ее математическое ожидание (если оно неизвестно). Такого типа задачи решаются в математической статистике.

Замечание. Заметим, что во всех приведенных теоремах 1 – 4 справедлива на самом деле и более сильная сходимость в среднем квадратическом.

Действительно,

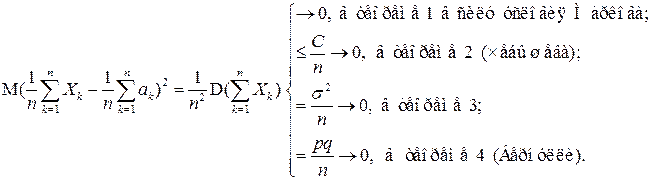Пример. Пусть 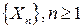- последовательность случайных величин, дисперсии которых ограничены одной и той же постоянной 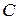, а коэффициент корреляции любых случайных величин 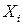и 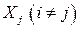, не являющихся соседними в последовательности, равен нулю. Подчиняется ли эта последовательность случайных величин закону больших чисел?

Решение. Проверим выполнение условия в теореме Маркова:

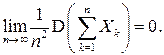
Из свойств дисперсии следует, что 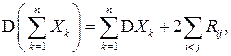где 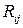- корреляционный момент случайных величин 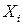и 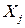. Но для 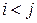, по условию, 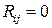, если . Следовательно, в сумме 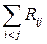равны нулю все слагаемые кроме, может быть, 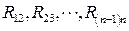(их ровно ).

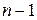Для любых 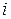и 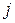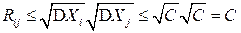, так как, по условию 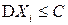для любого 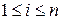. Поэтому

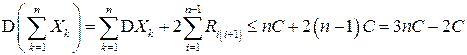
и получаем, что

.

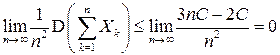Таким образом, последовательность случайных величин 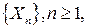подчиняется закону больших чисел.

Дата добавления: 2015-06-30; просмотров: 400; Нарушение авторских прав

Мы поможем в написании ваших работ!