Характеристические функции

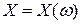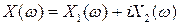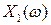Наряду с вещественными случайными величинами рассматриваются и комплекснозначные случайные величины, под которыми понимаются функции вида , где , и 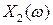- вещественнозначные случайные величины, называемые действительной и мнимой частями случайной величины 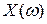соответственно. По определению при этом полагается, что 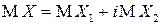и считается, что математическое ожидание 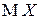существует, если существуют математические ожидания 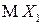и 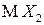. Отметим, что для математического ожидания комплекснозначной случайной величины остаются справедливыми все свойства М1) – М6) с очевидными изменениями.

Определение. Характеристической функцией вещественной случайной величины с функцией распределения 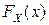называется комплекснозначная функция 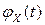действительной переменной, определяемая для любого 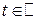равенством:

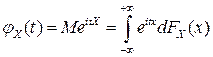. (4.21)

Вычисляется характеристическая функция в соответствии с основной теоремой о математическом ожидании по формулам:

если - дискретная случайная величина, принимающая значения 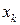с вероятностями 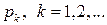, то

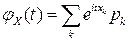; (4.22)

если - непрерывная случайная величина с плотностью вероятностей 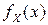, то

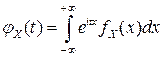. (4.23)

Характеристические функции представляют собой прекрасный аппарат для исследования свойств сумм независимых случайных величин и на их применении основаны доказательства многих предельных теорем.

Дата добавления: 2015-06-30; просмотров: 317; Нарушение авторских прав

Мы поможем в написании ваших работ!