
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Свойства характеристических функций
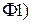 . Характеристическая функция
. Характеристическая функция 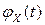 любой случайной величины
любой случайной величины  удовлетворяет условиям:
удовлетворяет условиям:
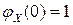 ,
, 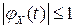 для любого
для любого 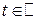 .
.
▲ 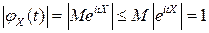 ■.
■.
В частности, из свойства 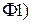 следует, что характеристическая функция существует у любой случайной величины
следует, что характеристическая функция существует у любой случайной величины  , в то время как просто математическое ожидание существует не всегда.
, в то время как просто математическое ожидание существует не всегда.
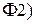 . Характеристическая функция
. Характеристическая функция 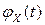 любой случайной величины
любой случайной величины  обладает свойством:
обладает свойством:
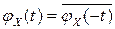 .
.
▲ 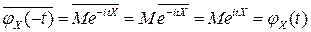 ■.
■.
В частности, из свойства 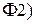 следует, что характеристическая функция случайной величины
следует, что характеристическая функция случайной величины  , имеющей симметричный относительно оси ординат закон распределения, является вещественной (в этом случае
, имеющей симметричный относительно оси ординат закон распределения, является вещественной (в этом случае 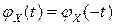 и поэтому
и поэтому 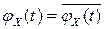 ).
).
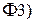 . Характеристическая функция
. Характеристическая функция 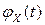 любой случайной величины
любой случайной величины  является неотрицательно определенной функцией, то есть для любого
является неотрицательно определенной функцией, то есть для любого 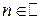 , для любых
, для любых 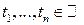 и любых комплексных чисел
и любых комплексных чисел 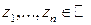
 .
.
▲ В соответствии с определением характеристической функции имеем: 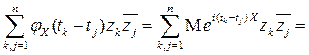
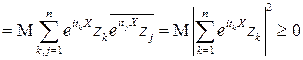 ■.
■.
Замечание. На самом деле справедливо более общее утверждение, известное как теорема Бохнера-Хинчина. Для того, чтобы непрерывная функция 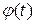 , удовлетворяющая условию
, удовлетворяющая условию 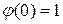 , была характеристической функцией, необходимо и достаточно, чтобы она была неотрицательно определенной (свойство
, была характеристической функцией, необходимо и достаточно, чтобы она была неотрицательно определенной (свойство 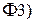 доказывает эту теорему в одну сторону).
доказывает эту теорему в одну сторону).
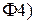 . Для любых вещественных чисел
. Для любых вещественных чисел 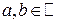
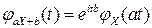
(преобразование характеристической функции при линейном преобразовании).
▲ Действительно, в соответствии с определением характеристической функции имеем:
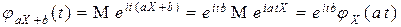 ■.
■.
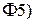 . Характеристическая функция суммы независимых случайных величин равна произведению характеристических функций слагаемых:
. Характеристическая функция суммы независимых случайных величин равна произведению характеристических функций слагаемых:
если 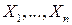 - независимые случайные величины, а
- независимые случайные величины, а 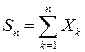 , то
, то
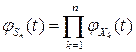 .
.
Свойство 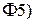 означает, что свертке законов распределения независимых случайных величин соответствует произведение их характеристических функций.
означает, что свертке законов распределения независимых случайных величин соответствует произведение их характеристических функций.
▲ В соответствии со свойствами математического ожидания имеем: 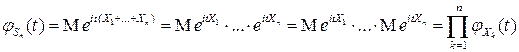 ■.
■.
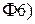 . Если у случайной величины
. Если у случайной величины  при некотором
при некотором 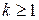 существует момент порядка
существует момент порядка 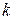 , то есть
, то есть 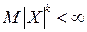 , то характеристическая функция
, то характеристическая функция 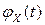 случайной величины
случайной величины 
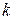 раз непрерывно дифференцируема и ее
раз непрерывно дифференцируема и ее 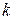 -я производная в нуле
-я производная в нуле 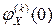 связана с моментом порядка
связана с моментом порядка 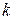 соотношением:
соотношением:
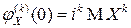 .
.
В частности, 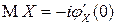 ,
, 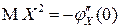 ,
, 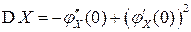 .
.
▲ Докажем свойство в непрерывном случае, когда случайная величина  имеет плотность вероятностей
имеет плотность вероятностей 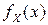 и ее характеристическая функция
и ее характеристическая функция
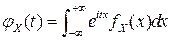 .
.
(в дискретном случае доказать самостоятельно).
Формальное дифференцирование характеристической функции 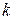 раз по
раз по 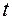 дает:
дает:
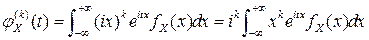 ,
,
откуда 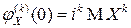 .
.
Законность дифференцирования под знаком интеграла определяется тем фактом, что
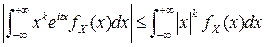
и существованием момента 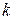 -го порядка ■.
-го порядка ■.
Замечание. При четном 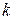 справедливо и обратное утверждение: если характеристическая функция случайной величины
справедливо и обратное утверждение: если характеристическая функция случайной величины  имеет производную
имеет производную 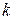 -го порядка в нуле
-го порядка в нуле 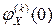 , то у нее существуют моменты
, то у нее существуют моменты 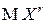 всех порядков
всех порядков 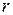 до
до 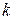 включительно и
включительно и 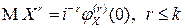 .
.
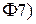 . Если у случайной величины
. Если у случайной величины  существует момент порядка
существует момент порядка 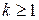 , то есть
, то есть 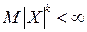 , то ее характеристическая функция
, то ее характеристическая функция 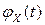 в окрестности точки
в окрестности точки 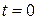 разлагается в ряд Тейлора:
разлагается в ряд Тейлора:
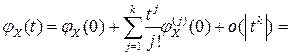
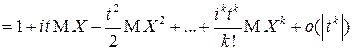 .
.
▲ Свойство 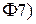 следует из свойства
следует из свойства 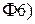 и определения ряда Тейлора ■.
и определения ряда Тейлора ■.
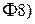 (формула обращения).
(формула обращения).
Если 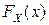 - функция распределения случайной величины
- функция распределения случайной величины  , а
, а 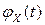 - ее характеристическая функция, то для любых двух точек
- ее характеристическая функция, то для любых двух точек 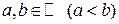 , в которых функция распределения
, в которых функция распределения 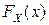 является непрерывной, справедливо равенство:
является непрерывной, справедливо равенство:
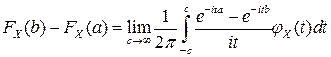 .
.
▲ Докажем свойство для непрерывной случайной величины  с плотностью вероятностей
с плотностью вероятностей 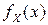 и абсолютно интегрируемой характеристической функцией
и абсолютно интегрируемой характеристической функцией 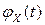 :
: 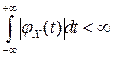 (общий случай см. в учебнике А.А. Боровкова «Теория вероятностей»).
(общий случай см. в учебнике А.А. Боровкова «Теория вероятностей»).
Поскольку в соответствии с (4.23) у непрерывной случайной величины  характеристическая функция
характеристическая функция 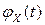 является преобразованием Фурье от плотности вероятностей
является преобразованием Фурье от плотности вероятностей 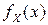 :
:
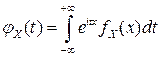 ,
,
то абсолютная интегрируемость 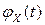 является достаточным условием существования обратного преобразования Фурье, в соответствии с которым
является достаточным условием существования обратного преобразования Фурье, в соответствии с которым
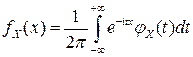 .
.
Интегрируя обе части последнего равенства по 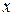 в пределах от
в пределах от 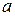 до
до 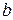 , получаем:
, получаем:
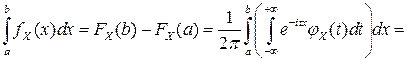
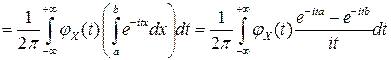 ,
,
что и доказывает формулу обращения в непрерывном случае ■.
Непосредственно из свойства 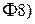 вытекают следующие утверждения.
вытекают следующие утверждения.
Следствие 1. Если характеристическая функция 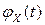 некоторой случайной величины
некоторой случайной величины  абсолютно интегрируема:
абсолютно интегрируема: 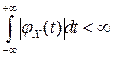 , то эта случайная величина является непрерывной и ее плотность вероятностей
, то эта случайная величина является непрерывной и ее плотность вероятностей 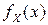 есть обратное преобразование Фурье от характеристической функции:
есть обратное преобразование Фурье от характеристической функции:
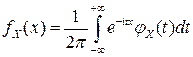 .
.
Следствие 2. Абсолютно интегрируемая функция 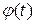 :
: 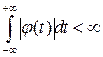 , удовлетворяющая свойствам
, удовлетворяющая свойствам 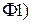 и
и 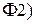 , является характеристической тогда и только тогда, когда ее преобразование Фурье всюду неотрицательно:
, является характеристической тогда и только тогда, когда ее преобразование Фурье всюду неотрицательно:
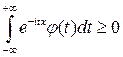 для любого
для любого 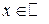 .
.
▲ В этом случае преобразование Фурье 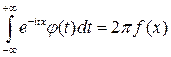 , где
, где 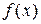 - плотность вероятностей некоторой непрерывной случайной величины
- плотность вероятностей некоторой непрерывной случайной величины  , являющаяся функцией неотрицательной для любого
, являющаяся функцией неотрицательной для любого 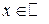 ■.
■.
Замечание. Фактически утверждение следствия 2 позволяет проверять свойство неотрицательной определенности абсолютно интегрируемой функции 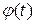 . Если функция
. Если функция 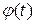 , удовлетворяющая свойствам
, удовлетворяющая свойствам 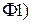 и
и 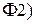 , абсолютно интегрируемой не является, но допускает представление в виде ряда Фурье
, абсолютно интегрируемой не является, но допускает представление в виде ряда Фурье 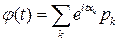 , то она является характеристической функцией (и, следовательно, обладает свойством неотрицательной определенности) дискретной случайной величины
, то она является характеристической функцией (и, следовательно, обладает свойством неотрицательной определенности) дискретной случайной величины  , принимающей значения
, принимающей значения 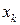 с вероятностями
с вероятностями 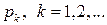 .
.
Следствие 3 (теорема единственности).
Характеристическая функция 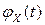 случайной величины
случайной величины  однозначно определяет ее функцию распределения
однозначно определяет ее функцию распределения 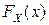 .
.
▲ Следует из формулы обращения 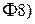 и того, что разности
и того, что разности 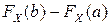 при любых
при любых 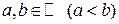 однозначно определяют функцию распределения
однозначно определяют функцию распределения 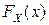 ■.
■.
| <== предыдущая страница | | | следующая страница ==> |
| Характеристические функции | | | Дискретные случайные величины |
Дата добавления: 2015-06-30; просмотров: 370; Нарушение авторских прав

Мы поможем в написании ваших работ!