Дискретные случайные величины

0. Вырожденная случайная величина.

Если 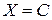п.н., то .

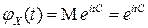1. Индикаторная случайная величина.

Индикаторная случайная величина имеет вид:

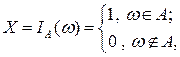
а ее закон распределения:

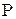
	q	p

где .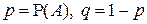

В соответствии с определением характеристической функции дискретной случайной величины (4.22) имеем:

.

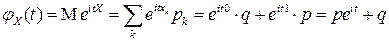Окончательно,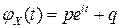

.

2. Биномиальная случайная величина .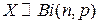

Множество возможных значений биномиальной случайной величины

,

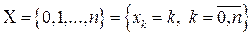а вероятности, с которыми значения принимаются, определяются по формуле Бернулли:

.

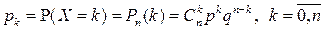Найдем характеристическую функцию случайной величины .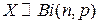

1 способ.

По определению характеристической функции и на основании бинома Ньютона имеем:

.

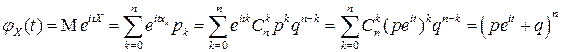2 способ.

В соответствии с представлением (4.20) случайная величина 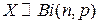равна сумме независимых случайных величин

,

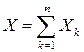где 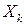- индикаторная случайная величина (число успехов в 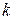-ом испытании), имеющая характеристическую функцию 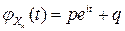, 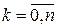. Поэтому по свойству .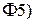

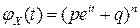Окончательно,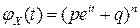

.

3. Геометрическая случайная величина .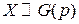

Множество возможных значений геометрической случайной величины

,

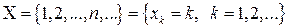а вероятности значений определяются по формуле:

.

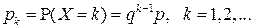Найдем характеристическую функцию случайной величины .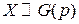

По определению характеристической функции и с учетом выражения для суммы бесконечно убывающей геометрической прогрессии имеем:

.

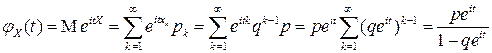Окончательно,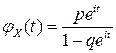

.

4. Пуассоновская случайная величина .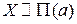

Множество возможных значений пуассоновской случайной величины

,

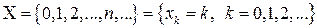а вероятности, с которыми значения принимаются, задаются формулой:

.

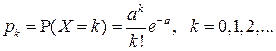Найдем характеристическую функцию случайной величины .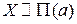

По определению характеристической функции и с использованием выражения для разложения экспоненты в ряд Тейлора имеем:

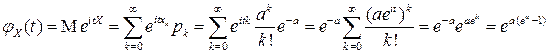
Окончательно,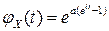

.

Используя характеристические функции, найдем числовые характеристики, например, геометрической случайной величины .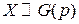

.

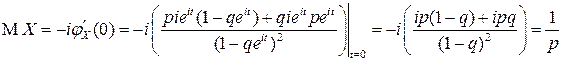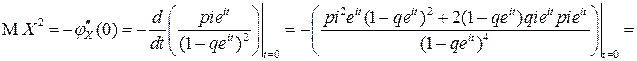
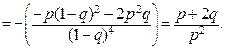
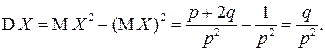
Найти с использованием характеристических функций числовые характеристики биномиальной и пуассоновской случайных величин самостоятельно.

Дата добавления: 2015-06-30; просмотров: 270; Нарушение авторских прав

Мы поможем в написании ваших работ!